Добротність коливальної системи

При вивченні коливальної системи без демпфірування, визначилися три інтегральні характеристики: амплітуда, частота власних коливань і початкова фаза. Для системи з демпфіруванням введемо четверту характеристику, що є кількісною мірою демпфірування: добротність коливальної системи Q.

Розглянемо вимушені коливання системи в усталеному режимі.

Відомо, що амплітуда коливальної швидкості при цьому має вигляд:

.

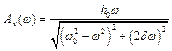Амплітудно-частотну характеристику зображено на рис.4.12.

Інтервал Δω=ω₂-ω₁ називають шириною резонансної кривої. Такий вибір інтервалу частот пов'язаний з виконанням наступної умови: кінетична енергія в системі не повинна зменшитися більше, як у 2 рази по відношенню до її максимального значення. Тоді добротність системи визначають наступним чином:

рис. 4.12

.

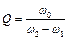Запишемо Δω=ω₂-ω₁ через параметри коливальної системи. Для цього підставимо в рівняння

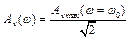
значення амплітуди коливальної швидкості. Тоді отримаємо:

;

;

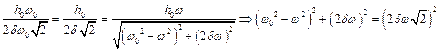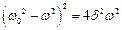
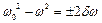
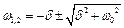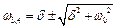
Фізичний зміст мають лише додатні корені, тоді припускаємо, що:

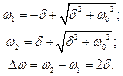
Звідси 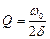-добротність системи та її характеристика демпфірування. Запишемо одне корисне співвідношення між логарифмічним декрементом згасання θ і добротністю Q:

.

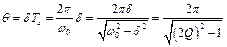При Q ≤ ½ власні рухи в системі не коливальні. Значення Q = ½ називають критичним (межа коливального режиму), як і відповідне йому значення δ=ω₀. У раз високої добротності (Q >> 1) 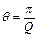або .

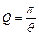Наведемо приклади величин добротності деяких типів згасаючих осциляторів: електричний контур – 50÷500;

гучномовець (на низьких частотах) – 3÷10;

рояльна чи скрипкова струна – 1000;

камертон – 3000;

п'єзоелектричний кристал – 500 000.