В) Власні затухаючі коливання

Загальний розв'язок диференціального рівняння, що описує вимушені коливання системи з урахуванням сил опору середовища (4.13) має вид

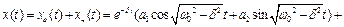
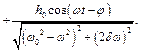
Перший доданок в цьому виразі описує коливальний процес в системі з одним ступенем вільності, якщо в ній під дією початкових умов збурені коливання і на систему діє сила опору середовища, пропорційна першому степеню швидкості:

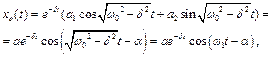
де , , .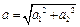

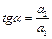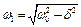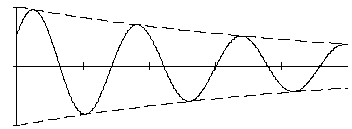
Залежність х₀(t) показана на рис.4.11.

рис. 4.11

Рух системи є затухаючим коливальним, але не періодичним, оскільки x₀(t)≠x₀(t+ T_з). Тому, умовно введемо поняття період T_з такого руху.

Періодом згасаючих коливань T_з (рис.4.11) називають проміжок часу [t₁;t₂] між двома послідовними проходженнями тіла (точки) через положення статичної рівноваги в певному фіксованому напрямку.

У положенні статичної рівноваги (t₁,t₂,t₃,…,t_s на рис.4.11) cos(ω₁t-α)=0. Оскільки ω₁T_з=2π, то .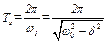

Звідси видно, що період згасаючих коливань більший за період незгасаючих коливань, тобто опір середовища, що пропорційний першому степеню швидкості, збільшую період коливань.

Дослідимо максимальні відхилення а₀, а₁, а₂, що відповідають моментам часу t₀, t₀+T_з, t₀+2T_з.

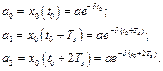
Знайдемо відношення максимальних відхилень:

.

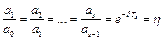Таким чином, амплітуда згасаючих коливань у разі в'язкого тертя (сила опору, пропорційна першому степеню швидкості) спадає за геометричною прогресією. Величину η (знаменник геометричної прогресії) називають декрементом згасання (або фактором згасання), а модуль натурального логарифма цієї величини 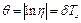- логарифмічним декрементом згасання коливань.

Поняття про декремент згасання коливань використовують при експериментальному визначенні коефіцієнта опору середовища.

Підводячи підсумок, зазначимо, що для системи з в'язким тертям слід розрізняти три характерні частоти:

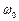- частота власних незатухаючих коливань;

1. 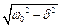- частота власних затухаючих коливань;

2. 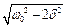- резонансна частота за зміщенням;

3. 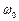- резонансна частота за швидкістю.