Принцип Даламбера-Лагранжа. Загальне рівняння динаміки
Принцип Даламбера дає можливість поширити принцип можливих переміщень на випадок руху системи. Дійсно, якщо до точок системи прикласти сили інерції, то можна вважати, що система перебуває у стані рівноваги. Тоді можна застосувати принцип можливих переміщень. У результаті дістанемо принцип Даламбера-Лагранжа.
Якщо на систему накладено ідеальні в’язі, то сума робіт активних сил і сил інерції на можливих переміщеннях точок системи буде від’ємною або дорівнюватиме нулю:
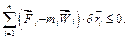 (3.6)
(3.6)
Як і раніше, знак нерівності стосується можливих переміщень, що зводять точки системи з однобічних в’язей.
При відсутності однобічних в’язей із нерівності (3.6) дістанемо рівність, яка називається загальним рівнянням динаміки:

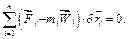 (3.7)
(3.7)
Впроваджений термін пояснюється тим, що з цього рівняння, як наслідок, випливають основні рівняння руху системи, а також основні теореми динаміки.
Приклади
1. Балка АВ (рис.3.8) спирається в точках А та В на шарнірно-рухому і шарнірно-нерухому опори і знаходиться під дією двох сил ( 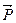 і
і 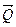 ), прикладених в точках С і D(AC=CD=DB=a). Кут
), прикладених в точках С і D(AC=CD=DB=a). Кут 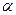 відомий. Користуючись загальним рівнянням статики, визначити реакцію опори В.
відомий. Користуючись загальним рівнянням статики, визначити реакцію опори В.
Скористаємось аксіомою про звільнення від в’язей і прикладемо в точці силу В, яку приєднаємо до вже відомих активних сил. Розглянемо балку АВ як систему з ідеальними двобічними в’язями. Надамо точкам системи можливих переміщень: 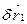 ,
, 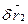 ,
, 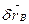 . Застосовуючи загальне рівняння статики (4.3), дістанемо
. Застосовуючи загальне рівняння статики (4.3), дістанемо
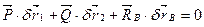 (а)
(а)
або
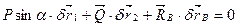 (b)
(b)
Встановимо зв’язок між 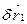 ,
, 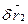 ,
, 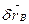 . Елементарні геометричні обчислення дають змогу знайти
. Елементарні геометричні обчислення дають змогу знайти
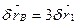 ;
; 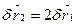 .
.
Тоді вираз (b) запишеться у вигляді
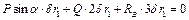
Після очевидних спрощень знайдемо
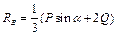
2. На подвійному блоці знаходяться ланцюги, які підтримують тягарі 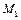 і
і 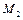 (рис.3.3). Знайти кутове прискорення блока, нехтуючи його масою і масами ланцюгів, якщо вага тягарів відповідно
(рис.3.3). Знайти кутове прискорення блока, нехтуючи його масою і масами ланцюгів, якщо вага тягарів відповідно 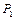 і
і 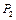 .
.
Припустимо, що 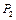 >
> 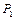 . Напрями прискорень тягарів дають змогу визначити напрями сил інерції
. Напрями прискорень тягарів дають змогу визначити напрями сил інерції 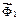 і
і 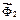 .Надамо точкам системи можливих переміщень
.Надамо точкам системи можливих переміщень 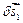 ,
, 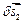 і скористаємося загальним рівнянням динаміки
і скористаємося загальним рівнянням динаміки
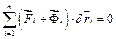
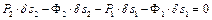 (с)
(с)
Залежність між 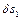 і
і 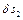 така :
така :
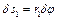 ;
; 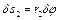 . (d)
. (d)
Сили інерції
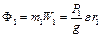 ;
; 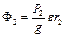 . (е)
. (е)
Підставляючи (d) і (e) до (с) , маємо
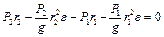 ,
,
звідки
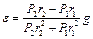 .
.
Дата добавления: 2020-08-31; просмотров: 990;











