Рівняння рівноваги системи матеріальних точок в узагальнених координатах (Рівняння Лагранжа другого роду)

Розглянемо рівняння рівноваги системи матеріальних точок в узагальнених координатах. У випадку рівноваги системи робота, виконувана на можливих переміщенняхточок системи, має бути рівна нулю

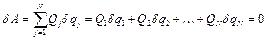. (а)

Рівняння (а) має виконуватись при довільних пиреміщеннях точок системи, вимірюються приростом узагальнених координат 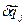. Користуючись незалежністю узагальнених координат 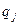та довільністю їх вимірювань 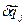, покладемо

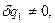
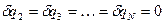. (b)

Тоді рівняння (а) матиме вид

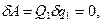(c)

звідки випливає, що Q₁ = 0.

Аналогічно доводиться, що у випадку рівноваги системи всі узагальнені сили рівні нулю

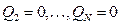(d)

Тобто 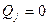, 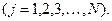(3.22)

Рівності (3.19) виражають у найбільш загальному вигляді рівняння рівноваги системи матеріальних точок та абсолютно твердих тіл. Із (3.22) випливають умови рівноваги у найбільш загальному вигляді: система матеріальних точок буде знаходитись у рівновазі, якщо узагальнені сили рівні нулю.

Усі розглянуті раніше умови рівноваги є лише частковим випадком цих загальних умов рівноваги.

Повернімося до розгляду задач динаміки. Використавши принцип Деламбера, можна із рівнянь рівноваги (3.22) отримати рівняння руху. Для цього додамо до діючих на систему сил сили інерції, введучи їх у рівняння (3.22). Тоді для рухаючоїсь системи рівняння (3.22) можна записати як рівняння руху

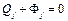
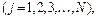(3.23)

де Ф_j – узагальнена сила інерції, котру на основі (3.16) можна представити так

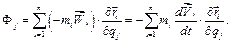(e)

Перетворивши вираз (e) для узагальненої сили інерції отримаємо рівняння Лагранжа другого роду:

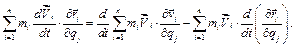(f)

Розглянемо суми, що входять у (f). На основі (3.13) знайдем

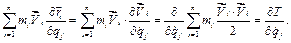(g)

Перетворимо і другий доданок виразу (f)

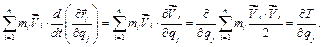(h)

Підставивши (g) та (h) у (e), отримаємо вираз для узагальненої сили інерції

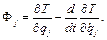(i)

Взявши до уваги (i), можна написати рівняння руху (3.23) у розгорнутому вигляді

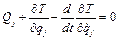
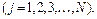
Інакше ці рівності можна записати так

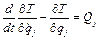
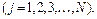(3.24)

Система рівнянь руху (3.24) називається системою рівнянь Лагранжа другого роду. Ці рівняння є передовими не лише в теоретичній механіці, а й інших розділах теоретичної фізики (рівняння тяжіння Ейнштейна, рівняння Максвела в електродинаміці і т.і.).

Рівняння Лагранжа другого роду – система звичайних диференціальних рівнянь другого порядку відносно узагальнених координат 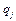. Кількість рівнянь Лагранжа другого роду рівна числу ступенів вільності системи N.

Розв'язавши рівняння Лагранжа другого роду, знайдемо закон руху системи, а потім за принципом Деламбера визначаємо реакції в’язей.