Правило визначення моменту сили відносно осі.
Щоб знайти момент сили відносно осі, треба спроектувати вектор сили на площину, перпендикулярну осі, і, розглядаючи проекцію як вектор деякої сили, знайти момент цієї проекції відносно точки перетину осі з площиною.
Це правило дозволяє знайти величину моменту сили відносно осі.
Момент сили відносно осі додатній, якщо спостерігачу, який дивиться з додатнього напрямку осі здається, що вектор 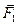 намагається надати тілу обертання проти годинникової стрілки. Якщо спостерігачу здається, що сила
намагається надати тілу обертання проти годинникової стрілки. Якщо спостерігачу здається, що сила 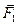 намагається надати тілу обертання за годинниковою стрілкою, то знак моменту сили відносно осі від'ємний.
намагається надати тілу обертання за годинниковою стрілкою, то знак моменту сили відносно осі від'ємний.
Розглянемо випадки обертання в нуль моменту сили відносно осі.
1. Момент сили відносно осі рівний нулю, якщо проекція сили на площину, перпендикулярну осі, рівна нулю, тобто 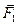 =0 у виразі (2.44).
=0 у виразі (2.44).
2. Момент сили відносно осі рівний нулю, якщо лінія дії сили перетинає вісь. Тоді в виразі (2.44) h=0.
Обидва випадки можна об'єднати: момент сили відносно осі рівний нулю, якщо вектор сили та вісь розміщені в одній площині.
Все сказане дозволяє стверджувати, що момент сили відносно осі рівний проекції моменту сили відносно точки на цю вісь (рис.2.27):
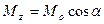 (2.45)
(2.45)
Повернемося до розглянутих вище аналітичних умов рівноваги вільного твердого тіла (2.41) та (2.42) та сформулюємо їх: вільне тверде тіло знаходиться в рівновазі, якщо виконуються шість аналітичних умов рівноваги (алгебраїчні суми проекцій сил на три координатні вісі мають дорівнювати нулю та алгебраїчні суми моментів сил відносно тих самих осей мають бути рівні нулю).

|
| рис.2.28. |
Приклад.
Кришка прямокутного ящика ABCD утримується з одного боку паличкою DE. Вага кришки 120 Н, AD=AE, кут DAE=60°. Визначити реакції шарнірів А та В, а також зусилля S в паличці, нехтуючи її вагою (рис.2.28)
Розв'язок. Обираємо тіло, рівновагу якого потрібно розглянути. Очевидно, це кришка ящика. Обираємо систему координат так, як це показано на рис.71. Проаналізувавши сили, прикладені до кришки (вага кришки Р=120 Н), знайдемо реакції шарнірів та зусилля в паличці S. Напрямки реакцій шарнірів невідомі, тому ми розкладемо їх на складові по координатним осям, припускаючи, що проекції реакцій додатні. Невідомі сили завжди вважаємо направленими в додатній бік осей. Після розв'язку рівнянь рівноваги з'ясовується їх дійсний напрямок. Складові реакцій вздовж осі Oy рівні нулю, бо опори А та В не заважають переміщенню кришки вздовж осі Oy. Позначимо складові реакцій XA, ZA та XB, ZB. Складемо систему рівнянь рівноваги відповідно до (2.41), (2.42):
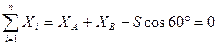 (a)
(a)
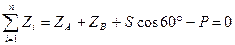 (b)
(b)
Сума проекцій сил на вісь Oy тотожньо рівна нулю. Знайдемо суми моментів сил відносно координатних осей
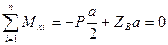 ; (c)
; (c)
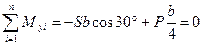 ; (d)
; (d)
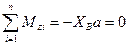 . (e)
. (e)
Розв'яжемо систему рівнянь рівноваги. З рівняння (f) отримаємо XB=0.
З рівняння (d) знайдемо 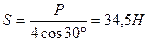 .
.
З рівняння (e) знайдемо 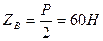 .
.
З рівняння (b) отримаємо 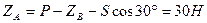 .
.
З рівняння (a) визначаємо 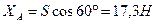 .
.
Дата добавления: 2020-08-31; просмотров: 994;











