Момент сили відносно осі

Розглядаючи систему рівнянь (2.42), прийдемо до поняття про момент сили відносно осі.

Припустимо, задана декартова система координат Oxyz, сила 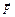, проекції якої на осі координат рівні X, Y, Z, та координати точки прикладання сили x, y, z. Розглянемо фізичний зміст проекції моменту сили на вісь Oz:

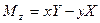. (2.43а)

З рівності (2.43а) видно, що якщо переміщувати точку прикладання сили паралельно осі Oz, то права частина (2.43а) не зміниться, бо в неї не входить змінна координата z. Якщо ж змінювати положення початку координат на осі Oz, величина М_z також не зміниться. Тобто, М_z не залежить від розташування центру моментів на осі Oz. Величина М_z залежить лише від взаємного розташування вектора сили 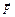та всієї осі Oz. М­_z та аналогічно величини

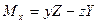, (2.43b)

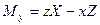(2.43c)

називають моментами сили відносно осей Oz, Оx та Oy.

Знайдемо момент сили відносно осі Oz, не звертаючись до аналітичної формули (2.43а). Спроектуємо вектор сили 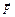на площину Oxy та позначимо проекцію 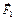(рис.2.27). Знайдемо моменти, створювані силою 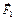відносно координатних осей

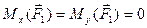, (2.43d)

бо для сили 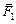координата z та проекція Z рівні нулю.

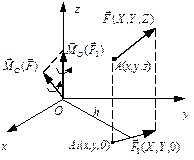
рис.2.27.

На основі (2.43d) робимо висновок, що повний момент сили 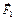відносно осі Oz по своїй величині рівний моменту сили 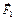відносно осі Oz, який визначається як добуток сили 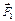на плече h:

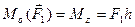. (2.44)