Дійсні та можливі переміщення. В'язі. Ступені вільності
Перед тим, як почати виклад фундаментальних положень, необхідно дати визначення поняттям, що входять до них.
Поняття про можливі переміщення належить до найважливіших понять механіки. Будемо розрізняти два види переміщень, що матимуть основне значення у подальшому, - можливі та дійсні переміщення.
Дійсні переміщення – це елементарні переміщення точок матеріальної системи, що відбуваються за певний проміжок часу під дією активних (заданих) сил.
Можливі переміщення – це нескінченно малі уявні переміщення, що відбуваються у фіксований момент часу і не суперечать накладеним в'язям.
Останнє поняття є кінематичне. Воно ніяк не пов’язане з діючими на систему точок силами. При наданні точкам системи можливих переміщень нестаціонарні в’язі необхідно вважати “зупиненими”, час фіксованим.
Існує ще і третій вид переміщень – здійснені переміщення - такі переходи точок системи з одного положення в просторі і часі в інші, які не суперечать накладеним в'язям. Час при цьому не фіксується, нестаціонарні в’язі не “зупиняються ”.
Дійсні переміщення відповідають дійсному закону руху системи і відбуваються під дією сил, прикладених до точок системи. Ці переміщення утворюють одну із систем здійснених переміщень.
Якщо матеріальна точка може залишити в'язь, то така в'язь називається однобічною або неутримуючою.
Якщо матеріальна точка не може залишити в'язь, то така в'язь називається двобічною або утримуючою.
Для знаходження можливих переміщень проводиться варіація функції за тими ж законами, що і диференціювання, тільки при цьому варіація часу δt=0.
Тут і далі позначатимемо вектор можливого переміщення 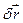 , здійсненного
, здійсненного 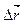 , дійсного
, дійсного 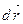 .
.
Ідеальною називається така в'язь, сума елементарних робіт яких на будь-яких можливих переміщеннях системи дорівнює нулю.
У випадку ідеальних в'язей дійсне переміщення є одним з можливих
Розглянемо властивості ідеальних в’язей, звернувшись до найпоширеніших прикладів: поверхня, стрижень, трос.
Нехай точка знаходиться на ідеально гладкій поверхні (рис.3.1).

| 
|
| рис. 3.1 | рис. 3.2 |
Реакція 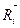 такої в’язі збігається з нормаллю до поверхні. Надамо точці можливого переміщення
такої в’язі збігається з нормаллю до поверхні. Надамо точці можливого переміщення 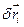 .
.
Вектор 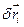 напрямлений по дотичній до поверхні, якщо точка залишається на ній
напрямлений по дотичній до поверхні, якщо точка залишається на ній 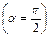 і утворює гострий кут з нормаллю, якщо точка покидає поверхню
і утворює гострий кут з нормаллю, якщо точка покидає поверхню 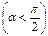 , тобто
, тобто 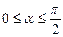 .
.
Обчислюємо елементарну роботу 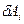 , яку виконує реакція в’язі
, яку виконує реакція в’язі 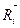 на можливому переміщенні
на можливому переміщенні 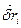 :
:
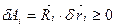 . (а)
. (а)
Якщо на поверхні знаходиться система точок, то вираз (а) набуває вигляду
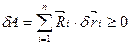 (b)
(b)
Знак нерівності відповідає випадку, коли точки покидають в’язь.
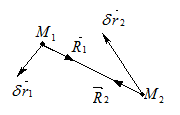
Розглянемо приклад стримуючої в’язі – дві матеріальні точки, з’єднані абсолютно твердим стрижнем (рис.3.2).
Надамо точкам можливих переміщень 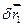 і
і  і обчислимо елементарну роботу реакцій
і обчислимо елементарну роботу реакцій 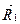 і
і 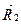 на цих переміщеннях. Для цього скористаємось теоремою про роботу сил, що діють на абсолютно тверде тіло. Внаслідок того, що сили
на цих переміщеннях. Для цього скористаємось теоремою про роботу сил, що діють на абсолютно тверде тіло. Внаслідок того, що сили 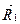 і
і 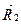 рівні за модулем і протилежні за напрямом, їх головний вектор і головний момент дорівнюють нулю:
рівні за модулем і протилежні за напрямом, їх головний вектор і головний момент дорівнюють нулю:
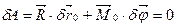 (с)
(с)
Поверхня – однобічна в’язь, тому  , стрижень – двобічна, тому
, стрижень – двобічна, тому 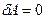 .
.
Узагальнимо отриманіі результати.
Сума робіт реакцій ідеальних в’язей на можливих переміщеннях точок системи – величина додатна або рівна нулю:
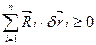 (3.1)
(3.1)
Знак рівності у виразі (3.1) відповідає наявності двобічних в’язей і таких можливих переміщень, що звільняють точки системи від цих в’язей.
Принцип Даламбера
Повернімося до вивчення задач динаміки. Розглянемо принцип Даламбера, який тісно пов’язаний зі статикою і є її подальшим розвитком.
Закони Ньютона встановлені для вільної матеріальної точки і вільної матеріальної системи. Між тим більшість матеріальних систем, з якими зустрічаються на Землі, невільні. Наукові дослідження у XVIII і XIX ст. в області механіки були направлені на те, щоб розповсюдити закони руху, знайдені для вільних систем, на вивчення руху систем невільних. У працях вітчизняних вчених Я.Германа (1716 р.) і Л. Ейлера (1736 р.) були вказані методи, які дозволяють вирішувати задачі динаміки для невільних матеріальних систем. Незалежно від цих вчених декілька пізніше французький вчений Даламбер (1743 р.) сформулював принцип, який увійшов у механіку під назвою «принцип Даламбера». Доказ, запропонований Даламбером, був громіздкий, але він спростився у XIX столітті, коли була встановлена аксіома про звільнення від в’язів. Перейдем до доведення принципу Даламбера. Розглянемо систему, яка складається з матеріальних точок з масами 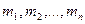 (рис.3.3). Якщо вона невільна, відкинемо в’язі та замінимо їх дію силами, рівними реакціям в’язей.
(рис.3.3). Якщо вона невільна, відкинемо в’язі та замінимо їх дію силами, рівними реакціям в’язей.

|
| Рис. 3.3 |
На рис.3.3 покажемо прикладені до кожної точки системи рівнодійну активних сил 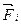 і рівнодійну реакцій в’язей
і рівнодійну реакцій в’язей 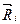 . Так як кожна точка системи після цього буде вільна, застосуємо для кожної точки системи другий закон Ньютона
. Так як кожна точка системи після цього буде вільна, застосуємо для кожної точки системи другий закон Ньютона
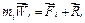 (
( 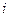 =1,2,…,n) (a)
=1,2,…,n) (a)
Формально перепишемо рівність (а):
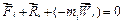 , (
, ( 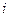 =1,2,…,n) (b)
=1,2,…,n) (b)
Рівності (b) виражають принцип Даламбера. Вони показують, що векторна сума трьох доданків: рівнодійної активних сил 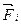 , рівнодійної реакції в’язей
, рівнодійної реакції в’язей 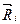 і доданку
і доданку 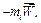 для всіх точок системи рівна нулю. При виконанні рівностей (b) система буде знаходитися у рівновазі.
для всіх точок системи рівна нулю. При виконанні рівностей (b) система буде знаходитися у рівновазі.
Позначимо доданок
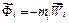 (3.2)
(3.2)
і назвемо його силою інерції. Тоді рівності (b) набудуть вигляду
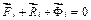 (
( 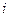 =1, 2, …,n). (3.3)
=1, 2, …,n). (3.3)
і будуть виражати принцип Даламбера. Кожна рівність системи (3.3) формально є умовою «рівноваги» сил, якщо вважати, що сила інерції також прикладена до рухомої точки. Але насправді рівноваги нема, точки системи рухаються. Тому принцип Даламбера формулюється так: активні сили, які діють на точки системи і реакції в’язей «зрівноважуються» силами інерції.
Розглянемо більш докладно силу інерції.
1. Із (3.2) видно, що сила інерції направлена у сторону, протилежну прискоренню точки.
2. Сила інерції не прикладена до матеріальної точки. Якщо б вона була прикладена до точки, то точка б зупинилась. На основі третього закону Ньютона можна зробити висновок, що сила інерції виникає внаслідок протидії точки.
 - головний вектор сил протидії, прикладених до тіл, які є джерелом активних сил і реакцій в’язей.
- головний вектор сил протидії, прикладених до тіл, які є джерелом активних сил і реакцій в’язей.
Із цього означення випливає:
1) якщо точка системи знаходиться у взаємодії із декількома тілами, то реально існують складові сили інерції, а сама вона, дорівнює векторній сумі реальних сил, але прикладених до різних тіл, фіктивна. Якщо на точку діє одне тіло, то сила інерції, прикладена до цього тіла, реальна;
2) так як сила інерції прикладена не до точки, а до в’язі, рівновага системи, що визначається рівняннями (3.3), уявна або фіктивна.
Принцип Даламбера – простий наслідок законів Ньютона і аксіоми про звільнення від в’язів.
Механіку можна побудувати і без принципу Даламбера, але він має велике практичне значення, так як дозволяє формально зводити задачі динаміки до задач статики, що суттєво спрощує їх розв’язок. Принцип Даламбера найбільш доцільно застосовувати при розв'язуванні першої задачі динаміки, коли невідомими величинами є сили.
При розв’язанні другої задачі динаміки також можна застосовувати принцип Даламбера: він дозволяє дуже легко скласти диференціальні рівняння руху. Ця методика складання диференціальних рівнянь руху має місце у механіці суцільних середовищ: у теорії пружності, опору матеріалів, гідравліці і т.п. При цьому складають рівняння рівноваги, після того приписують силу інерції і отримують рівняння руху.
Розглянемо приклади.
1 приклад. На тросі підвішений тягар М. Це може бути, наприклад, кабіна ліфту, прикріплена до тросу. Кабіна ліфта вагою 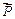 опускається униз із прискоренням
опускається униз із прискоренням 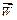 . Потрібно знайти натяг тросу
. Потрібно знайти натяг тросу  (рис. 3.4).
(рис. 3.4).
Розв’язання. Зробимо аналіз сил, прикладених до кабіни ліфту: сила ваги 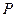 , натяг
, натяг 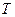 і умовно вважаємо прикладеною силу інерції
і умовно вважаємо прикладеною силу інерції
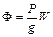 .
.
Згідно із принципом Даламбера кабіна під дією сил 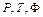 повинна знаходитися у рівновазі. Всі сили діють по прямій, тому достатньо скласти одне рівняння рівноваги.
повинна знаходитися у рівновазі. Всі сили діють по прямій, тому достатньо скласти одне рівняння рівноваги.
Проведемо вісь 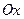 , обравши її початок у закріпленій точці
, обравши її початок у закріпленій точці 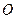 . Прирівняємо до нуля суму проекцій всіх сил на вісь
. Прирівняємо до нуля суму проекцій всіх сил на вісь 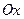 :
:
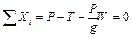 ,
,
звідки знайдемо натяг тросу
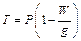 .
.

| 
|
| pис. 3.4 | pис.3.5 |
2 приклад. Два грузи вагою 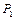 і
і 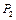 підвішені до тросів подвійного блоку (рис.3.5). Припустимо, що
підвішені до тросів подвійного блоку (рис.3.5). Припустимо, що 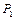 >
> 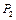 . При такій умові блок не буде знаходитись у рівновазі. Необхідно знайти кутове прискорення
. При такій умові блок не буде знаходитись у рівновазі. Необхідно знайти кутове прискорення 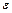 , з яким буде обертатися блок. Масу блока при цьому не враховувати. Радіуси блоків
, з яким буде обертатися блок. Масу блока при цьому не враховувати. Радіуси блоків 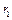 і
і 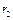 .
.
Розв’язання. Троси рухаються поступально, прискорення всіх точок тросів однакові. Якщо у місці контакту з блоком немає сковзання тросу, то прискорення дорівнює тангенціальному прискоренню при обертанні тіла навколо нерухомої осі 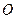 :
:
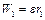 ;
; 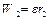 . (c)
. (c)
Знаючи прискорення вантажів знайдемо сили інерції
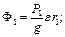
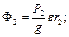 (d)
(d)
Складемо рівняння рівноваги за принципом Даламбера, прирівнявши до нуля суму моментів всіх сил відносно точки 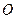 :
:
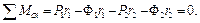 (e)
(e)
Підставивши (d) у (e), отримаємо:
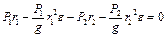 . (f)
. (f)
Звідси знайдемо
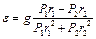 .
.
Дата добавления: 2020-08-31; просмотров: 1176;











