Диференціальне рівняння руху точки у векторному вигляді
При векторному способі задання руху точки (рис.2.8) прискорення виражається формулою
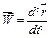 . (b)
. (b)
Другий закон Ньютона при цьому можна записати так:
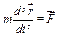 . (c)
. (c)

|
| рис.2.8 |
У частковому випадку вектор сили 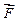 може бути сталим за модулем і за напрямом. Якщо вектор сили змінюється, то він може залежати від багатьох змінних: від часу, від розташування точки в просторі, від радіус-вектора
може бути сталим за модулем і за напрямом. Якщо вектор сили змінюється, то він може залежати від багатьох змінних: від часу, від розташування точки в просторі, від радіус-вектора 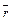 . Прикладом сил, залежних від розташування точки, є сили всесвітнього тяжіння, електростатичні, магнітностатичні, сили притягання і відштовхування. Сили опору середовища, в якому відбувається рух, залежать від швидкості руху точки. Сили опору залежать також і від прискорення точки
. Прикладом сил, залежних від розташування точки, є сили всесвітнього тяжіння, електростатичні, магнітностатичні, сили притягання і відштовхування. Сили опору середовища, в якому відбувається рух, залежать від швидкості руху точки. Сили опору залежать також і від прискорення точки 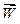 . Залежність сил від прискорення тут розглядатись не буде, так як такого типу сили зустрічаються рідко (наприклад, в електродинаміці).
. Залежність сил від прискорення тут розглядатись не буде, так як такого типу сили зустрічаються рідко (наприклад, в електродинаміці).
Рівняння (c) можна остаточно записати так
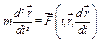 (2.5)
(2.5)
Диференціальні рівняння руху матеріальної точки у координатному вигляді
Припустимо, що на матеріальну точку М, що рухається діє система сил, рівнодійна яких рівна 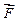 (рис.2.9).Проекції сили
(рис.2.9).Проекції сили 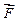 на осі координат позначимо X, Y, Z. Будемо користуватися прямокутною декартовою системою координат Oxyz. Положення точки на її траєкторії визначається у кожен момент часу координатами x, y, z.
на осі координат позначимо X, Y, Z. Будемо користуватися прямокутною декартовою системою координат Oxyz. Положення точки на її траєкторії визначається у кожен момент часу координатами x, y, z.

|
| рис.2.9 |
Щоб скласти диференціальне рівняння руху точки в координатному вигляді, спроектуємо праву і ліву частини рівності (2.5) на осі координат. При цьому слід пам’ятати, що проекції вектора швидкості точки на осі координат рівні першим похідним, а проекції прискорення точки рівні другим похідним за часом від координат точки, що рухається. Отримаємо:
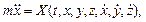
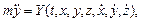 (2.6)
(2.6)
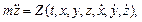
Невідомими функціями у (2.6) є координати точки як функції часу.
Дата добавления: 2020-08-31; просмотров: 849;











