Друга, або обернена, задача динаміки вільної матеріальної точки

Друга, або обернена, задача динаміки матеріальної точки складається з наступного: задані сили, що діють на точку, маса точки і початкові умови; знайти закон її руху.

Ця задача розв'язується інтегруванням диференціальних рівнянь руху точки. Для визначеності розглянемо диференціальні рівняння руху у координатній формі (2.6). Кожне з рівнянь системи (2.6) – диференціальне рівняння другого порядку. Загальний розв'язок системи (2.6) представимо відносно невідомих функцій x, y, z. У результаті інтегрування отримаємо координати x, y, z як функції часу і шести постійних інтегрування:

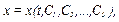
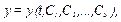(2.9)

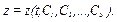
Розв'язок системи (2.9) неповний, так як невідомі постійні інтегрування, які визначаються із початкових умов. Початковими умовами називають значення координат точки і проекції її швидкості, що відповідають певному моменту часу :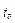

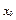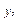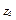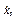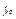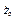, , , , , при 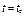. (2.10)

Шість початкових умов (2.10) дозволяють знайти шість постійних інтегрування. Для цього продиференціюємо за часом координати (2.9):

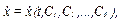
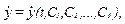(2.11)

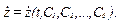
Потім у системи рівнянь (2.9) і (2.11) підставимо початкові умови (2.10) та отримаємо шість алгебраїчних рівнянь, з яких знайдемо шість невідомих .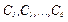

Підставивши значення постійних інтегрування у систему (2.9), знайдемо закон руху точки і остаточно розв'яжемо задачу.