Представление чисел в ЭЦВМ

Для представления двоичных чисел в цифровых ЭВМ используются две формы: с фиксированной запятой и с плавающей запятой.

При представлении чисел с фиксированной запятой положение запятой в разрядной сетке строго фиксируется, устанавливается определённое количество разрядов для целой и дробной частей числа и сохраняется неизменным на время вычисления для всех чисел. В большинстве случаев, машины оперируют с числами, по модулю меньше единицы. Положение запятой в этом случае фиксируется перед старшим разрядом числа. Для кодирования знака числа используется знаковый разряд, причём для ‘+’ ставится нуль, а для ‘-’ – единица. На рис. 4.1 приведена разрядная сетка, предназначенная для размещения чисел с фиксированной запятой.

Рис.4.1. Разрядная сетка, предназначенная для размещения чисел

с фиксированной запятой

Рис. 4.2. Разрядная сетка, предназначенная для размещения чисел

с плавающей запятой

Количество разрядов n определяет диапазон и точность представления чисел. Максимальное по абсолютной величине число изображается единицами во всех разрядах

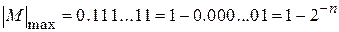
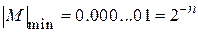
C помощью n разрядов числа и знакового разряда можно изобразить:

· отрицательные числа в диапазоне от –(1-2^-n ) до –2^-n;

· число нуль;

· положительные числа в диапазоне от 2^-n до (1-2^-n ).

Для того чтобы изобразить число, равное или превышающее по абсолютной величине единицу, необходимо вводить масштабный коэффициент k. Так, если 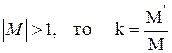, где 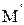– изображение числа М.

Подбор масштабных коэффициентов затрудняет подготовку задач для решения на машинах с фиксированной запятой.

Числа, меньшие, чем 2^-n, не могут быть представлены в машине и называется машинным нулём.

Машинный нуль для повышения точности вычислений округляется. Точность изображения числа М оценивается с помощью абсолютной и относительной погрешностей. Абсолютная погрешность не может превышать по величине единицы n+1 разряда:

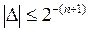
относительная погрешность, как известно, есть отношение абсолютной погрешности к величине числа М, то есть

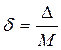
Для малых чисел величина 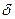может быть неприемлемой. Этого недостатка лишена вторая форма представления – нормальная.

В машине с плавающей запятой число в общем случае представляется в виде

,

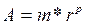где m – мантисса числа;

r – основание системы счисления;

p – порядок числа.

Для двоичной системы 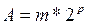. Порядок и мантисса могут быть как положительными, так и отрицательными, т.е. 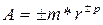. Для обозначения знака порядка и знака мантиссы в разрядной сетке машины отводятся специальные знаковые разряды, как показано на рис. 4.1 и 4.2.

Машины с плавающей запятой оперируют с нормализованными числами.

Число 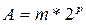называется нормализованным, если в старшем (первом после запятой) разряде мантиссы стоит единица, и ненормализованным, если стоит нуль.

При нормализации числа мантисса сдвигается влево на число разрядов, равное числу нулей до первой значащей цифры, и порядок числа уменьшается на количество сдвигов. В младшие разряды мантиссы записываются нули. Количество разрядов, отведённое под порядок числа, должно быть достаточным для обеспечения нормализации числа, представленного единицей младшего разряда мантиссы.

Пример 4.12.Нормализовать число

А = -0,0000101*10⁺¹¹⁰

Для его нормализации необходимо сдвинуть мантиссу влево на 4 разряда, а порядок уменьшить на 4 единицы. В нормализованном виде число примет вид

А = -0,1010000*10⁺⁰¹⁰

Количество разрядов сетки, отведённое для мантиссы, характеризует точность выполнения арифметических операций, количество разрядов сетки, отведённое для порядка, - диапазон представляемых чисел. Максимальное по модулю машинное число.

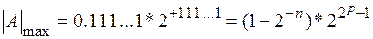
минимальное по модулю машинное число

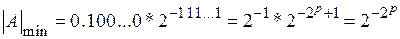
и, следовательно, диапазон чисел определится границами

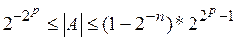
Как и в машинах с фиксированной запятой, выход за пределы верхней границы приводит к переполнению разрядной сетки, а выход за пределы нижней границы приводит к появлению машинного нуля, записываемого в виде всех нулей в разрядах мантиссы и порядка.

Абсолютная ошибка при округлении в младшем разряде

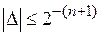
так как значения мантиссы лежат

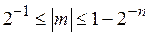
то минимальная и максимальная относительные погрешности

при больших n ;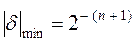

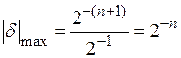
и

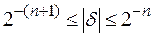
т.е. 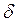не зависит от порядка числа, а точность представления и больших и малых чисел примерно одинакова.

Таким образом, нормальная форма представления чисел сравнительно с естественной имеет то преимущество, что при ней выше диапазон машинных чисел и точность их записи, однако представление чисел в естественной форме позволяет упростить схему машины и получить более высокое быстродействие.

Контрольные вопросы и задачи

4.1. Дайте определение непериодического сигнала.

4.2. Назовите основные характеристики случайных сигналов.

4.3. Постройте ряд распределения для вероятностей выпадения очков на гранях шестигранного игрального кубика.

4.4. Поясните выбор логарифмической функции для количественной оценки прироста информации.

4.5. Переведите целое десятичное число 189 в двоичную систему счисления.

4.6. Переведите десятичную дробь 0,625 в двоичную, восьмеричную и шестнадцатиричную системы счисления.

4.7. Определите в двоичном коде сумму чисел 9,5 и 12,25 и проверьте правильность выполнения операции путём перевода двоичной суммы в десятичную систему счисления.

4.8. Определите в двоичном коде разность (25,75-17,25).

4.9. Найдите произведение двоичных чисел 11011*101 и 101,01*10,11 и проверьте правильность выполнения операции умножения путём перевода двоичного числа в десятичную систему счисления.

4.10. При нормальной форме представления операндов количество разрядов, отведённое для мантиссы характеризует _____, а количество разрядов, отведённое для порядка характеризует ______.

Глава 5