Материальные носители информации
С технической точки зрения информация представляет собой объект передачи, хранения и преобразования в информационно-вычислительных системах (ИВС). В свою очередь, ИВС есть физическая система (устройство или комплекс устройств), предназначенная для автоматизации процесса алгоритмической обработки информации и вычислений. Физическими носителями информации являются сигналы, которые могут быть детерминированными и случайными, непрерывными и дискретными.
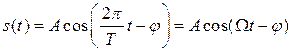 Детерминированным является сигнал, который может быть задан в виде некоторой определённой функции времени. Примерами детерминированного сигнала являются импульсы и пачки импульсов, форма, величина и положение во времени которых известны, а также непрерывный сигнал с заданными амплитудными и фазовыми соотношениями внутри его спектра. Детерминированные сигналы подразделяются на периодические и непериодические. Примером простейшего периодического детерминированного сигнала является гармоническое колебание вида
Детерминированным является сигнал, который может быть задан в виде некоторой определённой функции времени. Примерами детерминированного сигнала являются импульсы и пачки импульсов, форма, величина и положение во времени которых известны, а также непрерывный сигнал с заданными амплитудными и фазовыми соотношениями внутри его спектра. Детерминированные сигналы подразделяются на периодические и непериодические. Примером простейшего периодического детерминированного сигнала является гармоническое колебание вида
при 
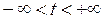 .
.
Через А, Т, 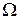 и
и 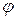 обозначены const: амплитуда, период, угловая частота и начальная фаза колебания соответственно.
обозначены const: амплитуда, период, угловая частота и начальная фаза колебания соответственно.
Так как любой сложный периодический сигнал может быть представлен в виде суммы гармонических колебаний с частотами, кратными основной частоте 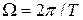 , то его основной характеристикой является спектральная функция, содержащая информацию об амплитудах и фазах отдельных гармоник.
, то его основной характеристикой является спектральная функция, содержащая информацию об амплитудах и фазах отдельных гармоник.
Если для детерминированного сигнала не существует конечного отрезка времени Т, отвечающего условию 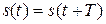 , то такой сигнал признаётся непериодическим.
, то такой сигнал признаётся непериодическим.
Случайные сигналы представляют собой случайные функции времени, для характеристики и анализа которых применяется статистический подход. Основными характеристиками случайных сигналов являются закон распределения вероятностей и спектральное распределение мощностей. Первый показатель исчерпывающе характеризует случайный сигнал, а второй позволяет получить распределение средней мощности сигнала по частотам, чего часто оказывается достаточно для анализа.
Дискретным признаётся сигнал, который может принимать лишь одно из конечного числа фиксированных значений (уровней). Для случайного дискретного сигнала каждому значению соответствует своя вероятность 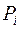 его осуществления. Такая таблица соответствия называется рядом распределения. Так как сигнал должен принять одно из возможных значений, то сумма вероятностей осуществления всех возможных событий
его осуществления. Такая таблица соответствия называется рядом распределения. Так как сигнал должен принять одно из возможных значений, то сумма вероятностей осуществления всех возможных событий
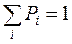 .
.
Непрерывным считается сигнал, который может принимать любое значение в интервале уровней. Для непрерывного случайного сигнала s вероятность того, что он примет определённое значение, бесконечно мала. В этом смысле целесообразно говорить о вероятности попадания s в какой-либо конечный интервал 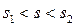 . Эта, так называемая «интегральная» вероятность определяется следующим образом
. Эта, так называемая «интегральная» вероятность определяется следующим образом
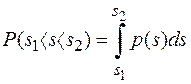 .
.
Функция 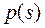 характеризует «дифференциальный» закон распределения вероятностей. Её ещё называют «плотностью вероятностей» непрерывной случайной величины s. При любом непрерывном распределении должно выполнять равенство
характеризует «дифференциальный» закон распределения вероятностей. Её ещё называют «плотностью вероятностей» непрерывной случайной величины s. При любом непрерывном распределении должно выполнять равенство
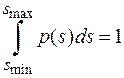 ,
,
где 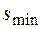 и
и 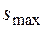 - соответственно нижняя и верхняя границы возможных значений s.
- соответственно нижняя и верхняя границы возможных значений s.
Для оценки информационной ёмкости сигнала должна быть установлена связь между параметрами сигнала и количеством информации, которое с помощью этого сигнала может быть передано. Информация содержится в сообщении, связанным с некоторым событием и является его описанием. Любое событие заключается в изменении во времени или в пространстве состояния объекта или процесса. Тогда сообщение является указанием на то, в каком состоянии находится объект или процесс. Пусть по каналу связи передаётся сообщение о событии, априорная вероятность которого равняется 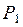 . После приёма сообщения апостериорная вероятность этого события для получателя становится равной
. После приёма сообщения апостериорная вероятность этого события для получателя становится равной 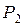 . Прирост количества информации, связанный с приёмом сообщения принято обозначать через
. Прирост количества информации, связанный с приёмом сообщения принято обозначать через
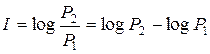 .
.
Выбор логарифмической функции для количественной оценки прироста информации даёт ряд преимуществ, главное из которых заключается в свойстве аддитивности: при передаче сообщений о независимых событиях полная информация оказывается равной сумме информаций, содержащихся в отдельных сообщениях. После неискажённого приёма сообщения вероятность 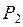 обращается в единицу и последнее выражение становится равным
обращается в единицу и последнее выражение становится равным
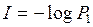 .
.
Таким образом, количество информации, содержащееся в передаваемом сообщении, зависит от вероятности 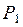 . Чем она меньше, т.е. чем больше неопределённость исхода, тем большая информация о нём получается в результате приёма сообщения. Если речь идёт о событии, имеющем два равновероятных исхода (например, бросание монеты), то
. Чем она меньше, т.е. чем больше неопределённость исхода, тем большая информация о нём получается в результате приёма сообщения. Если речь идёт о событии, имеющем два равновероятных исхода (например, бросание монеты), то 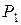 =0,5 и последнее выражение будет равно
=0,5 и последнее выражение будет равно
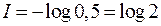 .
.
Численное значение I зависит от основания логарифма. Если в качестве последнего выбрать 2, то окончательно получим
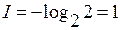 .
.
Определённая таким образом единица количества информации, соответствующая сообщению о том, что произошло одно из двух равновероятных событий, называется двоичной единицей информации или битом. Если одному из событий присвоить единичное значение, а второму – нулевое, получим двоичный алфавит.
Если с помощью этих двух символов, объединённых в позиционные коды, отображаются любые возможные сообщения, то речь идёт о цифровой двоичной форме представления информации и, соответственно, о цифровой схемотехнике.
В случае если эти же символы составляют так называемые вероятностные отображения любого сообщения, то речь идёт о вероятностной двоичной форме представления информации [13] и, соответственно, о вероятностной схемотехнике.
Первая форма представления дискретной информации сегодня везде: в компьютерной технике, микропроцессорных системах управления и автоматики, в бытовой технике и т.д., вторая известна значительно меньше, хотя имеет значительные перспективы развития в целом ряде отраслей современной информационной техники.
Представление дискретных сигналов в цифровой двоичной форме
Сегодняшний компьютер, микропроцессорная система управления или автоматики работают с информацией, представленной в цифровой двоичной форме. Минимальным информационным элементом является бит, принимающий значения 0 или 1. Биты организуются в более крупные кодовые комбинации: тетрады, байты, слова, т.е. 4-х, 8-и, 8хn – разрядные позиционные коды. С их помощью оказывается возможным закодировать любой необходимый для обработки символ. При обмене данными передается, как правило, символьная информация (буквы, цифры и другие знаки). Символы кодируются группой битов, число которых обычно лежит в пределах от 5 до 8. Если разрядность группы 5, то непосредственно можно отображать до 2 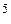 =32 различных символов. Такую разрядность имеет телеграфный код, в котором, однако, за счет дополнительных признаков принадлежности кода к той или иной регистровой группе число воспроизводимых символов расширено до 78.
=32 различных символов. Такую разрядность имеет телеграфный код, в котором, однако, за счет дополнительных признаков принадлежности кода к той или иной регистровой группе число воспроизводимых символов расширено до 78.
Международное признание получил американский стандартный код обмена информацией ASCII (American Standard Code for Information Interchange), в котором символы кодируются 7 двоичными разрядами. Этот код позволяет передавать цифры, прописные и строчные буквы латинского алфавита, целый ряд других символов (всего 96 символов, т. к. 32 кодовые комбинации выделены для представления команд обмена). На основе этого кода построен отечественный код КОИ-7 (код обмена информацией семиразрядный). Применяется также восьмиразрядный код ДКОИ-8. Внутри цифрового компьютера числа передаются в виде параллельных или последовательных позиционных кодов.
В позиционной системе счисления количественное значение каждой цифры зависит от ее места в числе (позиции), например 7382. Здесь первая цифра означает количество тысяч, вторая - количество сотен, третья - количество десятков и четвертая – количество единиц. Эти позиции называются разрядами числа. Для позиционной системы счисления справедливо равенство
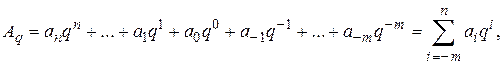
где 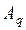 - произвольное число, записанное в системе счисления с основанием q;
- произвольное число, записанное в системе счисления с основанием q;
n+1, m – количество целых и дробных разрядов соответственно.
Каждая цифра в записанной последовательности может принимать одно из некоторого количества символов, используемых для изображения числа. Основание (базис) позиционной системы счисления - количество знаков или символов, используемых для изображения числа в разрядах данной системы счисления, оно и определяет название системы.
Вызванная к жизни не чем иным, как десятью пальцами пары человеческих рук, десятичная система использует 10 цифр
а (10)= {0,1,2,3,4,5,6,7,8,9}.
В цифровой технике используются только позиционные системы счисления. Наиболее распространены комбинированные (кодированные) – двоично-десятичная, двоично-восьмеричная, двоично-шестнадцатеричная и двоичная. В таблице 4.1 представлены эквиваленты десятичных цифр в указанных системах счисления.
Т а б л и ц а 4.1
| Десятичная цифра | Эквиваленты в системах счисления | Десятичная цифра | Эквиваленты в системах счисления | ||||
| Q=2 | Q=8 | Q=16 | Q=2 | Q=8 | Q=16 | ||
| A B C D E F |
В системе счисления с q = 2 для записи чисел используются цифры 0 и 1.
В системе счисления с q = 8 используют цифры 0 - 7.
В системе счисления с q = 16 обычно применяют следующие цифры и буквы: 0..9,A,B,C,D,E,F. Здесь A,B,C,D,E,F обозначают соответственно цифры 10,11,12,13,14,15.
Дата добавления: 2016-07-18; просмотров: 2084;











