Перевод чисел из одной системы счисления в другую

Перевод любого смешанного (т.е. содержащего целую и дробную часть) числа из одной системы счисления в другую может быть выполнен по универсальному алгоритму, состоящему из двух частей:

- последовательного деления целой части и образующихся целых частных на основание новой системы счисления;

- последовательного умножения дробной части и дробных частей получающихся произведений на основание новой системы счисления.

При переводе целой части числа в ходе процесса последовательного деления получаются остатки, которые представляют собой цифры целой части числа в новой системе счисления. Последний остаток является старшим разрядом переведенного числа.

При переводе дробной части числа при каждом умножении получаются целые части, которые исключаются из последующих умножений, и представляют собой цифры дробной части числа, переведенной в новую систему счисления. Значение первой целой части является первой цифрой после запятой переведенного числа.

Пример 4.1. Перевести число 356,1875₁₀ в восьмеричную систему счисления.

Перевод целой части Перевод дробной части

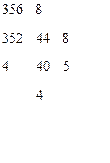
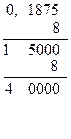
Пример 4.2. Перевести число 30,6₁₀ в двоичную систему счисления. Дробную часть переводить до четвертого знака после запятой.

Согласно универсальному алгоритму перевода чисел из одной системы счисления в другую переводим отдельно целую и дробную части числа:

Перевод целой части Перевод дробной части

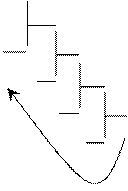
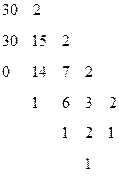
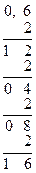
Результат 30,6₁₀ = 1110,1001_2.

Пример 4.3. Перевести десятичное число 691,15 в шестнадцатеричную систему счисления.

Перевод целой части Перевод дробной части

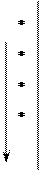
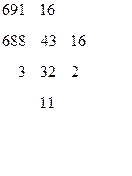
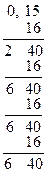
Результат 691,15₁₀ = 2B3,2666…_16.

При переводе целой части на втором шаге в остатке от деления получилось число 11, которое в символах шестнадцатеричного набора (см. табл.4.1) записывается как B.

Для перевода числа из любой системы счисления в десятичную удобно воспользоваться развернутой формулой его записи. Такой метод получил название метода непосредственного замещения.

Пример 4.4. Перевести двоичное число 100101,011 в десятичную систему счисления.

Представим данное число как сумму степеней числа 2, взятых с указанными коэффициентами:

100101,011 ₂ = 1*2⁵+0*2⁴+0*2³+1*2²+0*2¹+1*2⁰+0*2^-1+1*2^-2+1*2^-3 =

= 32+4+1+0,25+0,125 = 37,375 ₁₀.

Пример 4.5. Перевести восьмеричное число 703,04₈ в десятичную систему счисления.

Представим число в виде полинома с основанием 8:

703,04₈ = 7*8²+0*8¹+3*8⁰+0*8^-1+4*8^-2 = 7*64+3+0,25 = 451,0625 ₁₀.

Пример 4.6. Перевести шестнадцатеричное число B2E,4₁₆ в десятичную систему счисления.

Воспользуемся методом непосредственного замещения. Символы шестнадцатеричного алфавита, которые отсутствуют в десятичной системе счисления заменим на соответствующие им числа (см.табл.1):

B2E,4 ₁₆ = 11*16²+2*16¹+14*16⁰+4*16^-1 = 2862,0625₁₀.

Выбор восьмеричной и шестнадцатеричной систем счисления объясняется тем, что основания 8 и 16 есть целые степени числа 2, т.е. 8 = 2³ и 16 = 2⁴, благодаря чему перевод чисел из этих систем счисления в двоичную весьма прост. Достаточно заменить каждую цифру восьмеричного числа соответствующей ему (см. табл. 4.1) двоичной триадой (группой из трех двоичных цифр), а каждую цифру шестнадцатеричного - тетрадой (группой из четырёх двоичных цифр).

Для обратного перехода поступают следующим образом: двигаясь от точки, разделяющей целую и дробную часть, влево и вправо разбивают двоичное число на триады (тетрады), а затем заменяют их соответствующей восьмеричной (шестнадцатеричной) цифрой.

Пример 4.7. Перевести восьмеричное число 453,21 в двоичную и шестнадцатеричную системы счисления.

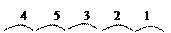Так как основание искомой системы счисления есть целая степень числа 2 (8=2³), заменим каждую восьмеричную цифру соответствующей ей двоичной триадой:

453,21 ₈ = 100 101 011,010 001 ₂

Для перевода в шестнадцатеричную систему этого числа, следуя от точки влево и вправо, разобьем его на тетрады и каждую тетраду заменим соответствующей шестнадцатеричной цифрой. В случае неполной тетрады можно дополнить число с краев нулями, что не изменит его значения:

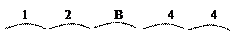0001 0010 1011, 0100 0100₂ = 12B,44₁₆

От того, какая система счисления будет использована в УОДИ, зависят скорость вычислений, емкость памяти, сложность алгоритмов выполнения арифметических и логических операций. В подавляющем большинстве случаев в ЭВМ применяют двоичную систему счисления, так как для представления в компьютере разряда двоичного числа может быть взят любой простой элемент, имеющий два надежно различимых устойчивых состояния, которые фиксируются напряжениями различного уровня, наличием или отсутствием импульса тока и т.п. Другим важным достоинством двоичной системы является простота двоичной арифметики. Недостатком двоичной системы счисления является громоздкая запись чисел. Для упрощения записи используют восьмеричную и шестнадцатеричную системы счисления.