Динамика груза, подвешенного к крану на трех канатах (трифилярный подвес груза)
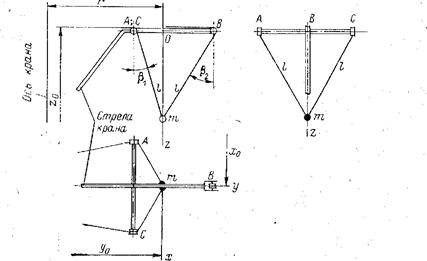
Рассмотрим трифилярный подвес груза, выполненный по схеме рис. 108, и только применительно к общему случаю колебаний. При этом будем предполагать, что точки подвеса А, В и С в процессе их периодических перемещений, вызванных качкой, остаются всегда в одной горизонтальной плоскости. Такое предположение вызвано тем, что в кранах треугольник ABC располагается самым различным образом, что не позволяет составить
единые уравнения, годные для всех конструкций. Поэтому здесь дается общая методика расчета, которая может быть легко преломлена применительно к каждому конкретному случаю.
Все частные случаи, подробно разобранные в § 42 и 41, здесь применимы практически без изменений. Так, например, отклонение груза от вертикали на угол у0 при равномерном повороте крана с угловой скоростью ωкр может быть рассчитано по формуле
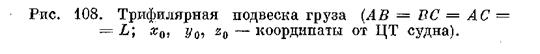
(12). При этом, как видно из рис. 103 и 108, отклонения может не быть, если

или
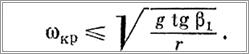
Отклонение груза от вертикали на угол φmaх при внезапном прекращении поворота крана приближенно (т. е. без учета влияния угла у0) может быть рассчитано по формуле (23). Что же касается колебаний, то для этого вполне достаточно рассмотреть только общий их случай.
При периодических перемещениях точек подвеса, происходящих, например, по закону (17), колебания груза будут описываться уравнениями (18), что видно из сопоставления рис. 108 и 109. Решение уравнений (18) связано с большими трудностями, вытекающими из необходимости следить в процессе расчета за положением груза, так как в зависимости от положения груза его
колебания могут происходить относительно шести различных центров: точек А, В, С и осей АВ, ВС, АС. Расчет существенно упростится, если рассматривать отдельно колебания от продольной качки и от поперечной. В этом случае расчетными уравнениями будут выражения (19) и (20).
В большинстве случаев трифилярная подвеска груза применяется в кранах, имеющих механизм слежения за вертикальными перемещениями палубы обслуживаемого судна. Будем называть
обслуживающим то судно, на котором установлен кран или передающее устройство канатной дороги; второе судно, участвующее в процессе приема — передачи груза, будем называть обслуживаемым. При наличии механизма слежения закон изменения координаты q в уравнениях (18)—(20) будет зависеть не только от скорости механизма подъема vM, но и от совместных вертикальных перемещений нока стрелы крана (центра трифиляра ABC) и палубы обслуживаемого судна. Если скорость механизма подъема крана vH постоянна, а закон вертикальной качки обслуживаемого судна задан, например, в виде
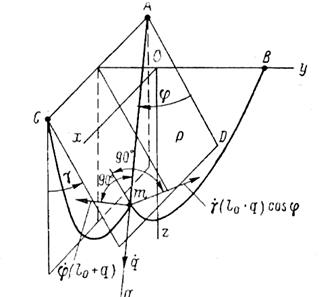
Рис. 109. Расчетная схема колебаний груза на трифилярной подвеске.

где m1 — амплитуда вертикальных перемещении, то

где z определяется по формуле (17), выражающей закон вертикальных перемещений нока стрелы крана.
Таким образом, при наличии механизма слежения колебания груза на трифилярной подвеске будут описываться уравнениями (18) или (19) и (20), в которых величину q и ее производные следует определять из выражения (32).
§ 44. Динамика канатных дорог
Принципиальные схемы канатных дорог представлены в гл. IV (см. рис. 46, 47, 49, 50, 51 и др.).
Предварительный расчет
На рис. 110 представлена наиболее распространенная схема канатной дороги с траверзным расположением передающих канатов: несущего и тяговых. Траектория движения грузовой тележки,
отмеченная на рис. 110 штриховой линией, в статике согласно [14, 22] определяется по следующим зависимостям: — на участке АС

где у, z — координаты в системе Ayz (рис. 110); 6 — угол уАВ, имеющий положительное значение при отсчете его от оси Ау по
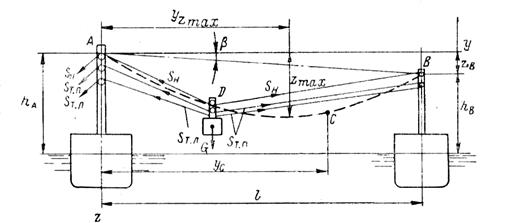
Рис. 110. Общая схема канатной дороги.
часовой стрелке и отрицательное при отсчете против часовой стрелки:
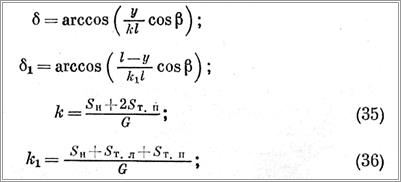
δ — расстояние между точками подвеса по горизонтали; Sн — натяжение несущего каната; Sт.п, ST,л— натяжение правой и левой ветвей тягового каната; G — вес передаваемого груза.
Схемным решением легко добиться (а это желательно) равенства k = k1 Тогда абсцисса точки С будет определяться по выражению
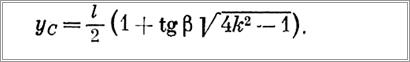
На участке АС натяжение канатов и тяговое усилие ST привода передвижения тележки без учета сил трения в ее ходовых частях определяются по формулам

Очевидно, что на участке АС тележка могла бы перемещаться самопроизвольно, а тяговое усилие ST играет здесь роль силы, удерживающей тележку от самопроизвольного движения. Условием такого движения от А до В является
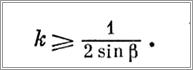
Расчет траектории движения тележки с грузом необходим для проверки прохождения груза над палубами и надстройками судна снабжения и корабля, над водой без окунания и захлестывания его волной, а также для определения формы приемных устройств, особенно в местах стыков жестких металлических рельсов с канатами. Из этого следует, что наиболее важно знать ординату максимального провисания груза zmax и ее абсциссу yzmах, а также форму начальных и конечных участков траектории. Исследования в [14] показали, что при положительных значениях угла В (наиболее вероятный случай) абсцисса yZmax всегда меньше абсциссы ус, а форма истинной (в статике) траектории движения грузовой тележки имеет вид, представленный на рис. 110.
На рис. 111 представлены зависимости Уzтах — f1(k,В,l) zmax = f2 (k,B,l), заимствованные из [14, 22]. Максимальные и значения тягового усилия без учета сил трения в ходовых частях грузовой тележки при положительных углах В, согласно [14], будут наблюдаться при нахождении тележки в точках А и В, причем 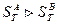 . Величины их могут быть определены по формулам (38), (40) или по зависимостям
. Величины их могут быть определены по формулам (38), (40) или по зависимостям

где yA и yB — углы наклона касательных к траектории движения грузовой тележки в точках А и В.
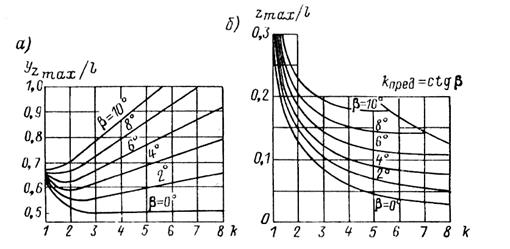
Рис. 111. Кривые зависимостей уzmax=f1(к, ϐ, l);zmax = f2 (к, ϐ ,l).
При проведении предварительного расчета очень удобным оказывается пользование графиками рис. 111. Пусть, например, заданы масса передаваемого груза G, расстояние между судами l, высоты над уровнем моря точек подвеса hA и hB и минимально допустимое расстояние груза от уровня моря hmin; требуется определить суммарное натяжение канатов.
Порядок расчета при этом следующий.
1. Находим zmax = hA — hmin и 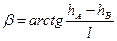 .
.
2. Определяем отношение zmax/l, после чего по этому отношению и найденному значению 6 по рис. 111, δ находим соответствующее им значение к. На рис. 111, а по k и B находим отношение Уzmaх/l и рассчитываем величину Уzmaх
3. По формуле (35) находим SH +2ST п = kG.
4. Найденное значение (SН + 2STП) умножаем на коэффициент динамичности кд, величину которого при предварительном расчете согласно [25] можно принять равной 1,4.
5. По формулам (33)—(44) можно рассчитать, если это требуется, остальные характеристики.
Дифференциальные уравнения движения грузовой тележки
Пусть тележка находится в произвольном положении, отмеченном на рис. 112 точкой D. Начало неподвижной прямоугольной системы координат xyz поместим в точку А. Масса тележки, сосредоточенная в точке D, имеет три степени свободы.
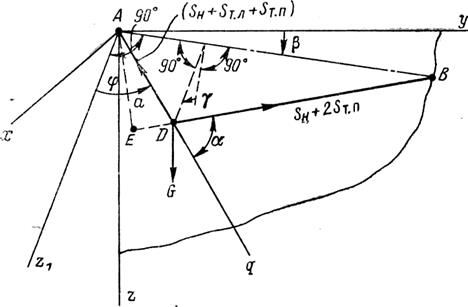
Рис. 112. Расчетная схема для канатной дороги.
В качестве обобщенных координат выберем: угол у, характеризующий отклонение плоскости треугольника ABD от вертикальной плоскости Ayz; угол φ, характеризующий отклонение ветви каната AD от оси Az1, лежащей в плоскости треугольника ABD и перпендикулярной к АВ; линейную координату q, совпадающую с ветвью каната AD и характеризующую ее удлинение, т. е. перемещение тележки в направлении от точки А. Обобщенные силы, соответствующие этим обобщенным координатам, будут
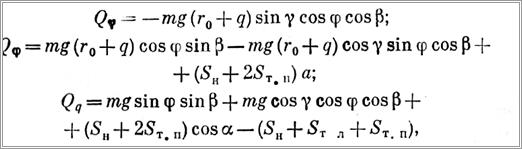
где r0 — отстояние тележки от точки А при t = 0; а и а — см, рис. 112, их значения будут даны ниже.
Проекции абсолютной скорости на оси х, у, z
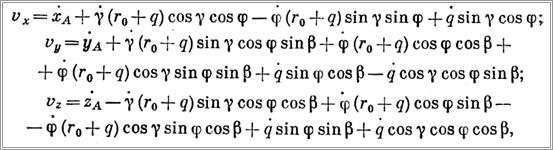
где хА, уА, zA — проекции переносной скорости, т. е. скорости перемещений точки подвеса А.
Следует заметить, что поскольку нами рассматривается движение тележки, происходящее с постоянной скоростью q = vт(vт — скорость, развиваемая тяговым приводом) относительно точки А, то при подсчете абсолютной скорости мы имеем право учитывать переносную скорость только точки А. Влияние перемещений на качке точки В учитывается при подсчете обобщенных сил Qφ и Qq содержащих величины а и а, зависящие от перемещений точки В.

Подставляя последовательно значения проекций скоростей и обобщенных сил в уравнения (9), (7) и (8), получим систему дифференциальных уравнений движения грузовой тележки по несущему канату в процессе качки судов
Система уравнений (45) может быть решена на ЭВМ. При этом первые два уравнения системы не зависят от третьего, поскольку закон изменения q во времени известен
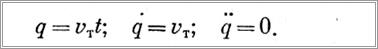
Входящие в систему уравнений величины а и а определяются по следующим зависимостям:
здесь l0 — расстояние между точками А и В по горизонтали на тихой воде; hA и hB — см. рис. 110; ув и zB — перемещения точки В на качке (влиянием хв пренебрегаем).
§ 45. Определение безопасного расстояния между судами, осуществляющими прием и передачу грузов с помощью траверзной канатной дороги.
Если два судна связаны между собой канатной дорогой, то на каждое из них при прямолинейном и равномерном движении действуют следующие силы (рис. 113):
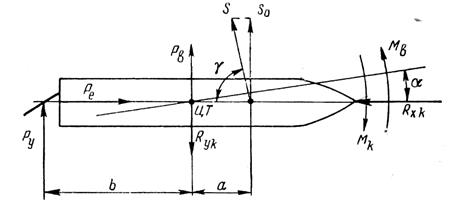
Рис. 113. К расчету безопасного расстояния между судами.
Ryk — нормальная к диаметральной плоскости составляющая гидродинамических сил, действующих на корпус судна;
Рy — нормальная к диаметральной плоскости составляющая гидродинамических сил, действующих на перо руля; Mk — гидродинамический момент; Рв и Мъ — соответственно поперечная сила и момент гидродинамического взаимодействия судов, характеризующие так называемое присасывание; S — проекция натяжения несущего и тяговых канатов на
горизонтальную плоскость; Ре — сила тяги винта; Rxk — сила сопротивления воды движению судна. При действии указанных сил составим два условия равновесия для равномерного прямолинейного движения судна
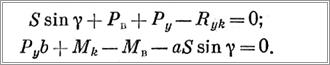
Подставляя в эти уравнения значения гидродинамических сил и моментов, указанные в [4, 13], после преобразований получим следующие уравнения:
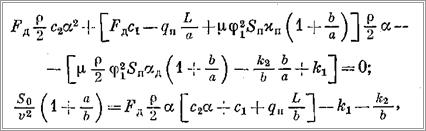
где FA — приведенная площадь диаметральной плоскости судна; р — массовая плотность воды; с1: с2 — коэффициенты нормальной силы; а — угол дрейфа судна; qп — коэффициент позиционного момента; L — длина судна; μ, — угловой коэффициент подъемной силы руля; ф1 — коэффициент влияния корпуса; хп — приведенный коэффициент влияния корпуса; Sa — приведенная площадь пера руля;

v — скорость судна; ад — допустимый угол отклонения пера руля от диаметральной плоскости [4, 13]; су и сm — гидродинамические коэффициенты (см. [13]).
Заметим, что полученные формулы справедливы при углах дрейфа, не больших 15°; для случая а = 0 (см. рис. 113) они непригодны; при решении квадратного уравнения относительно а следует брать только положительное значение корня уравнения (поскольку канат является односторонней связью, работающей только на растяжение).
Как видно из вышеизложенного, коэффициенты к1 и k2 определяют величину гидродинамических силовых факторов взаимодействия между судами (Рв и Мв). Результаты расчета величии k1

и к2 по формулам работы [13] в зависимости от расстояния между судами l представлены на рис. 114 и 115. Кривая 1 соответствует судам ПР «Профессор Баранов» — БМРТ «Пушкин», кривая 2 — TP «Прибой» — БМРТ «Пушкин», кривая 3—TP «Актюбинск» — БМРТ «Пушкин». Размерные характеристики этих судов:
| Судно | Наибольшая длина, м | Ширина, м | Осадка, м |
| БМРТ «Пушкин» | 84,87 | 13,4 | 3,9 |
| ПР «Профессор Баранов» | 21,3 | 8,125 | |
| TP «Актюбинск» | 130,91 | 16,8 | 6,26 |
| TP «Прибой» | 21,2 | 7,35 |
Из рис. 114 и 115 очевидно, что силы гидродинамического взаимодействия заметно уменьшаются при увеличении расстояния
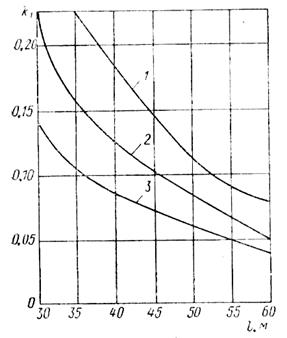
Рис. 114. Зависимость коэффициента к1от расстояния между судами l.
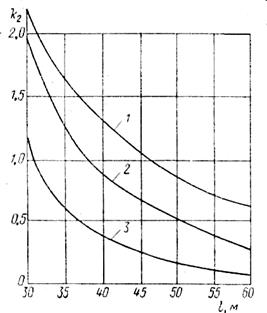
Рис. 115. Зависимость коэффициента к2от расстояния между судами I.
между судами. На расстоянии l >= 60 м они становятся незначительными. Полученные данные могут быть использованы (приближенно) и для других классов судов.
Определив безопасное расстояние, по уравнениям равновесия можно рассчитать требуемый угол дрейфа а и величину горизонтальной составляющей натяжения канатов S0 Для БМРТ типа «Пушкин» — представителя наиболее значительной серии судов рыбопромыслового флота — установлена более простая эмпирическая формула по определению допустимого значения величины S0 при 0,5≤a/b≤1
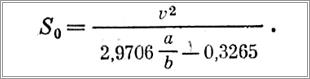
В заключение заметим, что величину а (см. рис. 113) следует брать как можно меньшей. При а < 0 (слева от ЦТ судна) достигается лучшая поворотливость судна, но натяжение канатов будет способствовать увеличению отклонения с курса.
Выводы
В настоящей главе рассмотрены вопросы расчета колебаний груза на регулярном морском волнении. Методы расчета колебаний на нерегулярном волнении рассмотрены в гл. VIII.
Динамический расчет трифилярных подвесок и канатных дорог получается весьма сложным. По мнению авторов, целесообразнее указанные устройства проверять на моделях. Методика моделирования и пересчета результатов модельных испытаний на натуру изложена в гл. IX.
Из расчетных уравнений (13), (15), (18)—(20) видно, что происхождение второго члена в них объясняется кориолисовой силой инерции. При этом при подъеме груза кориолисова сила инерции способствует раскачиванию груза, а при опускании играет роль силы сопротивления раскачиванию. Из этого следует, что опускать груз надо как можно с большей скоростью, а поднимать с малой скоростью. Для канатных дорог желательна большая скорость при удалении от точек А и В (см. рис. 110) и малая — при приближении к ним. Для количественной оценки влияния скорости на раскачивание груза с помощью ЭЦВМ было просчитано уравнение (15) для различных значений д0 и q = vM (скорость опускания). Величины полученных при этом угловых амплитуд φшах в радианах в первом цикле колебаний представлены ниже:
| vM, м/с | l0 = 3 м | l0 = 9 м | l0 = 15 м |
| 0,1166 | 0,2305 | 0,3123 | |
| 0,0748 | 0,1674 | 0,2378 | |
| 0,0554 | 0,1322 | 0,1936 |
Как видно из приведенных данных, наибольшая интенсивность уменьшения раскачивания наблюдается при скоростях до 5—6 м/с. Чем больше груз удален от нока стрелы, тем существеннее сказывается влияние скорости опускания на уменьшение величины амплитуды раскачивания. Расчет показал, что при подъеме груза увеличение скорости подъема приводит к значительному увеличению раскачивания; при скорости подъема vM = 10 м/с амплитуда раскачивания возрастает неограниченно.
Полученные данные хорошо согласуются с формулой И. И. Ольховского (Курс теоретической механики для физиков. Изд. второе. М., изд-во МГУ, 1974), которая при принятых здесь обозначениях будет иметь вид:

Для выявления эффективности бифилярных и трифилярных подвесок с помощью ЭЦВМ было просчитано первое уравнение из системы (19), полагая в нем х = хmcos ω t, хm = 1 м, φ = 1 1/c (эти данные примерно соответствуют продольной качке транспортного судна типа «Ленинский комсомол» D = 7690 т при волнении моря 5 баллов — см. [2]), z = 0 (влияние вертикальной качки не учитывается), q' = 0 (влияние скорости привода подъема не рассматривается).
Результаты расчета показали, что при данных условиях колебания груза на бифилярной подвеске в плоскости бифиляра, а на трифилярной подвеске в любой плоскости не возникают при следующих значениях величин L (расстояние между точками подвеса) и h (удаление груза от плоскости точек подвеса):
L, м........... 3 4 5 6
h, м........... 15 20 25 30
В то же время амплитуда раскачивания груза, подвешенного на одном канате, при этих же условиях достигает соответственно 15, 10, 7, 5°.
Следует отметить, что полученные расчетные данные были подтверждены моделированием. Результаты моделирования и анализ уравнений (19) позволяют рекомендовать следующую приближенную формулу оценки эффективности бифилярных или трифилярных подвесок:
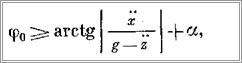
где а — амплитуда отклонения линии (или плоскости), проходящей через точки подвеса, от горизонтальной плоскости, обусловленная качкой судна.
Данная формула позволяет определить минимальное значение угла φ0 (половину угла между канатами подвески), исключающего раскачивание груза. Полученное по этой формуле значение угла в целях большей надежности следует увеличивать на 5—10%.
Глава VIII
ВЫПОЛНЕНИЕ ДИНАМИЧЕСКИХ РАСЧЕТОВ МЕТОДАМИ
ТЕРИИ ВЕРОЯТНОСТЕЙ
§ 47. Общие положения
Решение задач динамики связано с необходимостью составления дифференциальных уравнений, которые позволяют установить закон движения исследуемой системы тел или одного тела. Если дифференциальное уравнение учитывает все факторы, влияющие на изучаемое движение тела, то решение этого уравнения даст точный закон движения тела. Однако учесть все факторы, влияющие на движение, не всегда представляется возможным или оправданным. Это происходит, во-первых, из-за незнания природы отдельных действующих факторов. В этом случае такие факторы, если они существенны, учитываются приближенно. Во-вторых, некоторые факторы, мало влияющие на исследуемое движение, весьма усложняют само дифференциальное уравнение и его решение. В таких случаях этими несущественными факторами пренебрегают, примерами последних могут быть сопротивление воздуха, трение в шарнирах при изучении маятниковых колебаний и т. п.
Но даже при учете только существенных факторов могут получиться такие дифференциальные уравнения, которые не имеют точного аналитического решения, а решение их приближенными методами может оказаться весьма трудоемким. В таких случаях на помощь приходят методы теории вероятностей, и в частности, теория случайных функций. При решении задач динамики с помощью теории случайных функций, составляя дифференциальное уравнение движения изучаемого тела, возмущающую силу можно принимать изменяющейся по гармоническому закону с амплитудой, равной фактической. Дифференциальное уравнение при этом получится линейным с правой частью; аналитическое решение его известно. Методами теории вероятностей могут быть определены при нерегулярном волнении моря амплитуды качки судна, амплитуды перемещения характерных точек двух судов, амплитуды колебаний груза, подвешенного на крюке, и т. п.
§ 48. Краткие сведения из теории вероятностей
Случайные величины и их числовые характеристики
Поскольку мы будем пользоваться методами теории случайных функций, рассмотрим только те понятия и определения теории вероятностей, знание которых необходимо при изучении и применении теории случайных функций.
Случайная величина — такая величина, которая в результате опыта может принять то или иное заранее не известное значение. Случайные величины, принимающие только отдельные, изолированные друг от друга значения, которые можно заранее перечислить, называются прерывными, или дискретными, случайными величинами. Если же случайные величины не отделены друг от друга и могут непрерывно заполнять некоторый промежуток (зачастую бесконечный) их возможных значений, то такие случайные величины называются непрерывными.
Любую случайную величину полно характеризуют функция распределения и ряд распределения (для прерывной), или плотность распределения (для непрерывной). Однако при решении многих практических задач знание полной характеристики случайной величины не требуется, и вполне достаточно располагать отдельными числовыми параметрами, в некоторой мере характеризующими существенные черты распределения этой случайной величины.
Характеристики, которые позволяют выразить в сжатой форме наиболее существенные особенности распределения случайной величины, называются ее числовыми характеристиками.
Рассмотрим только те характеристики, знание которых потребуется нам в дальнейшем. Основной характеристикой положения случайной величины на числовой оси является ее математическое ожидание, которое иногда называют средним значением случайной величины.
Математическим ожиданием М (X), или тх случайной величины, называется сумма произведений всех возможных значений случайной величины на вероятности этих значений, т. е.

где xi — возможное значение случайной величины; pi — вероятность появления этого значения.
Формула (46) справедлива для прерывных случайных величин. Для непрерывных случайных величин

где f(х) — плотность распределения величины X.
Чтобы лучше понять физический смысл математического ожидания, заметим, что при большом числе опытов среднее арифметическое наблюденных значений случайной величины приближается (сходится по вероятности) к ее математическому ожиданию.
Мерой рассеивания значений случайной величины относительно ее математического ожидания является характеристика D (X), называемая дисперсией случайной величины

При вычислении дисперсий можно пользоваться формулами: — для прерывной величины
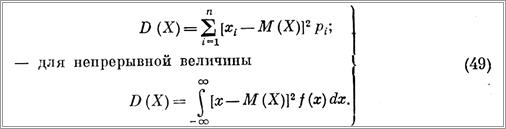
Дисперсия имеет размерность квадрата случайной величины. Величина называется среднеквадратичным отклонением случайной величины от математического ожидания.

Характеристики случайных функций
Случайной функцией X (t) называется такая функция, которая в результате опыта может принять тот или иной заранее не известный конкретный вид. Конкретный вид, принимаемый случайной функцией в результате опыта, называется ее реализацией. Группа опытов дает группу, или «семейство», реализаций случайной функции. Каждая реализация, естественно, представляет собой обычную (неслучайную) функцию. Следовательно, в результате опыта случайная функция превращается в обычную, неслучайную функцию. При некотором зафиксированном значении аргумента t функция X (t) превращается в обычную случайную величину, называемую сечением случайной функции, соответствующим моменту времени t.
При рассмотрении отдельных случайных величин случайного явления последнее изучается как бы «в статике». Теорию случайных функций в этом смысле, по образному определению Е. С. Вентцель, можно назвать «динамикой случайных явлений».
Характеристики случайных функций в общем случае представляют собой не числа, а функции.
Математическим ожиданием случайной функции X (t) называется неслучайная функция mх (t), которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции

По смыслу математическое ожидание случайной функции представляет собой некоторую среднюю функцию (рис. 116), около которой различным образом располагаются конкретные реализации случайной функции.
Дисперсией случайной функции X (t) называется неслучайная функция Dx (t), значение которой для каждого момента времени равно дисперсии соответствующего сечения случайной функции

Если для описания основных особенностей случайной величины достаточно знания математического ожидания и дисперсии, то для случайной функции этого уже будет недостаточно. Проиллюстрируем сказанное на примере рис. 116, на котором показаны реализации двух случайных функций Х1 (t) и Х2 (t),
имеющих примерно одинаковые математические ожидания и дисперсии. Характер же этих случайных функций совершенно различен: одна из них изменяется со временем плавно и постепенно, а другая — резко и быстро, имея вид неправильных, беспорядочных колебаний. Для случайной функции Х1 (t) значения одной и той же реализации в двух близлежащих сечениях примерно одинаковы, а для случайной функции Х2 (t) — различны и даже могут быть расположены по разную сторону от математического ожидания; Следовательно, для описания особенностей случайных функций нужна еще какая-то характеристика, учитывающая степень
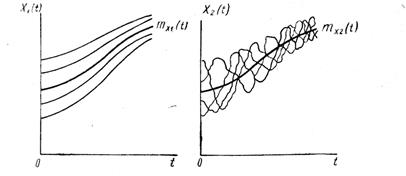
Рис. 116. Реализации двух случайных функций
зависимости между сечениями случайной функции, относящимися к различным моментам времени t. Такой характеристикой является корреляционная, функция.
Корреляционной функцией случайной функции X (t) называется неслучайная функция двух аргументов Кх (t; t'), которая при каждой паре значений моментов времени t, t' равна математическому ожиданию произведения [X (t) — mх (t)]*[X(t')—mх(t')]
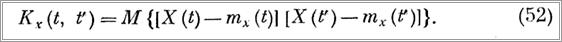
Очевидно, что при t = t' корреляционная функция, как это следует из сопоставления формул (48) и (52), обращается в дисперсию. Это позволяет сделать вывод о том, что в качестве основных характеристик случайной функции могут применяться только ее математическое ожидание и корреляционная функция.
Определение характеристик случайной функции из опыта
Для определения характеристик случайной функции X (t) над ней производители независимых опытов, в результате которых получается п реализаций этой функции. Каждая реализация находится путем подсчета случайных величин, соответствующих
этой реализации в моменты времени t1, t2, tm, равноотстоящие друг от друга. Таким образом, в результате опыта для всех реализаций находятся mn случайных величин. Математическое ожидание и дисперсия для каждого сечения случайной функции, т. е. для каждого момента времени tk, согласно [3], определяются по формулам


где xi (tk) — значение случайной величины, соответствующее i-й реализации в момент времени tk
Корреляционная функция для сечений к и l, соответствующих моментам времени tk и tl определяется по формуле
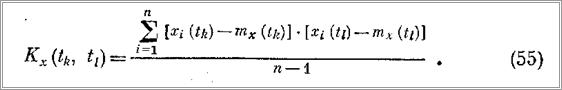
Определив математическое ожидание и дисперсию для каждого сечения, можно построить зависимости mх (t) и Dx (t) на графике, как это сделано, например, для mх (t) на рис. 116. Корреляционная функция Кх (t, t') как функция двух аргументов может быть воспроизведена только в пространственной (трехмерной) системе координат, в которой аргументы t и f' располагаются в одной плоскости, а сама корреляционная функция на оси, перпендикулярной этой плоскости.
Определение характеристик случайной функции по характеристикам исходной случайной функции
Определение характеристик случайной функции методом, указанным выше, не всегда возможно и целесообразно по следующим причинам:
— над проектируемым объектом (судно, прибор, система управления и т. п.) нельзя произвести опыты, поскольку сам объект еще не существует;
— постановка опытов над некоторыми объектами может оказаться весьма сложной и дорогостоящей;
— данные опыта, полученные на одном объекте, нельзя распространить на другие объекты, аналогичные, но не тождественные первому.
Поэтому теория случайных функций предлагает в подобных случаях не прямые, а косвенные методы исследования случайных функций. Сущность косвенного исследования случайных функций заключается в следующем. Рассмотрим это на примере качки судна. Качка судна обусловлена волнением моря. Поскольку волнение моря имеет резко выраженный неправильный («нерегулярный») характер, то процесс волнения моря можно отнести к категории случайных. Очевидно, что и качка судна под действием нерегулярного волнения также будет носить случайный характер. Введем
следующую терминологию. Исследуемые объекты (в нашем случае судно) будем называть динамической системой. Причину, вызывающую нарушение равновесия динамической системы, назовем воздействием (волнение моря), а сам результат выхода динамической системы из равновесного положения — реакцией динамической системы (качка судна).
Очевидно, что воздействие является исходной случайной функцией, а реакция — преобразованной случайной функцией. Будем считать, что динамическая система (рис. 117) осуществляет над входным воздействием некоторое преобразование, в результате которого исходная случайная функция X (t) преобразуется в другую случайную функцию Y (t). Символически это записывается так:
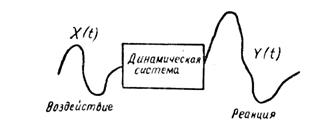
Рис. 117. Преобразование случайной функции динамической системой.

где А означает преобразование, которое для неслучайных функций х (t) и у (t) сводится к решению дифференциального уравнения, связывающего воздействие х (t) с реакцией у (t).
Из формулы (56) следует, что, зная характеристики исходной случайной функции и ее преобразование А, можно получить характеристики исследуемой преобразованной случайной функции. Например, зная характеристики волнения моря, можно определить характеристики качки не одного, а любого судна.
Для стационарных случайных процессов весьма удобный метод определения характеристик преобразованной случайной функции по характеристикам исходной случайной функции дает теория стационарных случайных функций (или процессов).
Случайная функция X (t) называется стационарной, если все ее вероятностные характеристики не зависят от выбора начала отсчета времени (например, волнение моря). Аргументом функции может быть не только время. Если же ее аргументом является время, то такая функция может быть названа процессом.
Для стационарной случайной функции, как следует т определения,
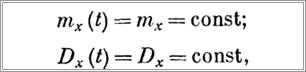
т. е. математическое ожидание и дисперсия не зависят от времени, а корреляционная функция зависит не от положения сечений t и t' = t + т, а только от промежутка т между первым и вторым сечениями, т. е.
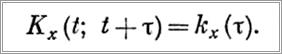
Спектральная теория стационарных случайных процессов основана на представлении случайных функций в виде спектральных разложений на гармонические колебания различных частот φ1, φ2, φk, причем амплитуды этих колебаний являются случайными величинами. Обычно спектр стационарной случайной функции описывает распределение дисперсий по различным частотам. Как следует из [3], дисперсия стационарной случайной функции равна сумме дисперсий всех гармоник ее спектрального разложения. Если по оси ординат откладывать дисперсии Dk, соответствующие своей частоте wk то мы получим «прерывистый», или «линейчатый», спектр дисперсий. Сумма ординат такого спектра равна дисперсии случайной функции. Если же по оси ординат откладывать не саму дисперсию Dk, а ее среднюю плотность, т.е. дисперсию, приходящуюся на единицу длины данного интервала частот φ, то получим ступенчатую диаграмму, высота которой на участке φ, прилежащем к точке φk, равна

и представляет собой среднюю плотность дисперсии на этом участке. Суммарная площадь всей диаграммы опять же будет равна дисперсии случайной функции.
Устремляя φ - О, из ступенчатой диаграммы получим плавную кривую Sx (φ), называемую спектральной плотностью дисперсии, или просто спектральной плотностью стационарной случайной функции. Очевидно, что кривая Sx (со) изображает плотность распределения дисперсий по частотам непрерывного спектра, а площадь, ограниченная этой кривой, равна дисперсии Dx случайной функции X (t)

Спектральная плотность Sx (со) описывает частотный (или амплитудно-частотный) состав стационарного процесса. Эта характеристика, однако, не является самостоятельной; она полностью определяется корреляционной функцией данного процесса.
Взаимосвязь между спектральной плотностью и корреляционной функцией стационарного случайного процесса определяется формулами
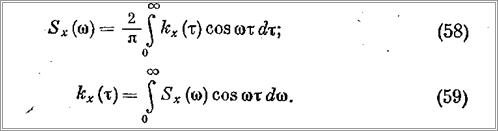
Для преобразования исходной стационарной случайной функции, согласно [3], достаточно только одно преобразование, а именно преобразование спектральной плотности входного процесса Sx (со). Очевидно, что это справедливо только для линейных динамических систем, т. е. для таких систем, которые описываются линейными дифференциальными уравнениями. Преобразование осуществляется по формуле
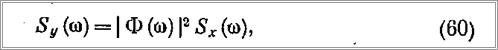
где |Φ (φ) |2 — квадрат модуля частотной характеристики системы, или, иначе, модуля передаточной функции; Sy (φ) — спектральная плотность выходного процесса.
Модуль передаточной функции | Φ (φ) | представляет собой коэффициент, который связывает амплитуды функций у (t). и х (t) в том частном случае, когда входная функция х (t) является гармонической и амплитуда ее равна единице. Например, в случае рассмотрения качки судна на нерегулярном волнении модуль передаточной функции можно найти как частное от деления выражения, полученного из решения линейного дифференциального уравнения качки, на соответствующую амплитуду волнения моря.
§ 49. Порядок решения задач динамики с помощью теории стационарных случайных функций
Рекомендуется следующий порядок решения.
1. Определяется модуль передаточной функции, для чего необходимо составить и решить дифференциальное уравнение, описывающее изучаемый процесс (уравнение должно быть линейным). Для качки судов передаточные функции определены в [2, 14, 22].
2. По формуле (58) определяется спектральная плотность на входе, т. е. воздействия. Спектральная плотность волнения моря может быть рассчитана по формулам работы [2] или же взята в готовом виде из [16].
3. По формуле (60) рассчитывается и строится кривая спектральной плотности на выходе системы (например, качки судна).
4. По формуле (57) или <
Дата добавления: 2020-08-31; просмотров: 1017;











