Принимающее судно; 2 - передающее судно; 3 - кранцы; 4 — креплениекранцев. 10 глава

Выразим перемещения точки подвеса О от качки судна через декартовы координаты

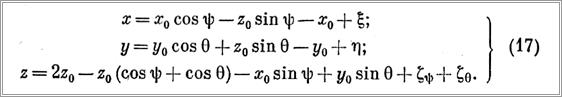
Таким образом, мы установили закон перемещений точки подвеса каната в процессе качки судна. При решении практиче­ских задач уравнения (16) необходимо составлять так, чтобы в рас­смотрение вошел наиболее неблагоприятный случай, который мо­жет быть выражен, например, следующим образом:

Вследствие непрерывного перемещения точек подвеса груз начнет совершать колебания (кинематическое возбуждение). Для составления дифференциальных уравнений колебаний груза при­меним метод Лагранжа. Поскольку рассматривается случай пере­менной длины каната, то груз будет иметь три степени свободы. В качестве обобщенных координат выберем: угол у, характеризу­ющий положение плоскости Р (рис. 105, в), проходящей через ка­нат, и ось О'х', параллельную Ох; угол φ , характеризующий откло­нение каната в плоскости Р от линии O'D, совпадающей при y = 0 с отвесным положением; линейную координату q, направлен­ную вдоль каната и характеризующую его удлинение.

Обобщенные силы, соответствующие своим обобщенным коор­динатам, выразятся следующим образом:

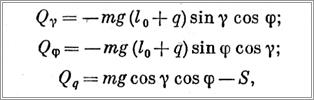
где l₀ — длина каната в момент времени t = 0.

Проекции скоростей на оси декартовой системы отсчета

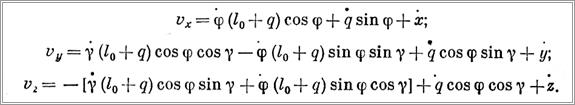
Найдя по формуле (9) абсолютную скорость груза и вычислив по первой формуле (7) его кинетическую энергию, используя формулы (8), получим дифференциальные уравнения колебаний груза

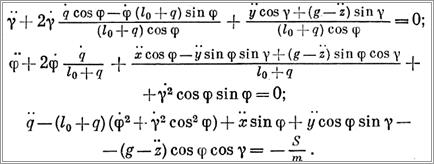
Решение системы уравнений (18) может быть выполнено на ЭВМ. Если удлинение каната происходит с постоянной скоростью, т. е. q = v_M - const, то первые два уравнения системы становят­ся независимыми от третьего; их решение позволит исследовать колебания груза, решение же третьего уравнения даст возможность установить закон изменения натяжения каната.

Практически при грузовых операциях судно испытывает раз­дельно или продольную качку (при постановке на якорь) или поперечную (в дрейфе на больших глубинах, когда постановка на якорь неосуществима). Поэтому с целью упрощения расчета систему уравнений (18) можно разделить на две:

— для продольной качки (θ = 0, £е = 0, η = 0, у = 0)

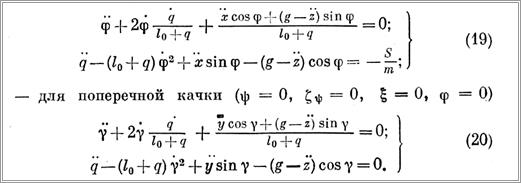
В системах (19) и (20) при q = v = const первые уравнения будут также независимыми от вторых. Решение их на ЭВМ, на­пример, методом Рунге — Кутта не вызывает никакой сложности.

§ 42. Динамика груза, подвешенного к крану на двух канатах (бифилярный подвес)

Схема бифилярного подвеса груза представлена на рис. 106. Рассмотрим некоторые особенности его расчета для случая, когда плоскость бифиляра перпендикулярна вертикальной плоскости Р, проходящей через ось стрелы крана.

Равномерный поворот крана при постоянном вылете стрелы

Расчет углов у₀ и радиуса - р (см. рис. 103) при бифилярном подвесе производится по формулам

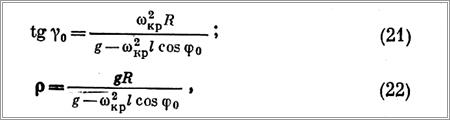
справедливым (см. § 41) при

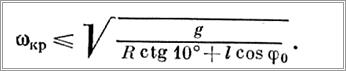
Натяжение канатов S равно

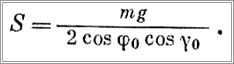
Внезапное прекращение поворота крана

Пусть в момент остановки крана груз имел линейную ско­рость v (см. рис. 106). Принимая допущение об абсолютной не­упругости каната, можно считать, что на отклонение груза от положения равновесия (т. е. на подъем груза) будет затрачена только та часть кине­тической энергии груза 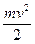,кото­рая обусловлена скоростью v₁ =v соs_φ0, т.е. 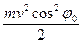. Другая

часть кинетической энергии, обусло­вленная скоростью v₂ = v sin φ, т. е.

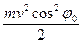, будет полностью израсхо­дована на деформацию каната. Заме­тим, что

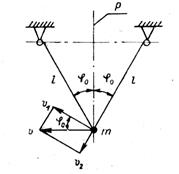
Рис. 106. Бифилярный под­вес груза.

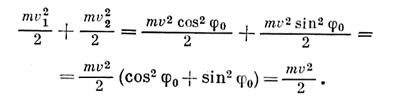
Пренебрегая углом у₀ (см. рис. 103) и деформацией каната, используя теорему об изменении кинетической энергии, найдем

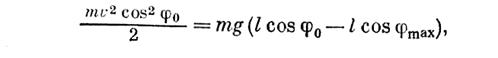
откуда угол максимального отклонения груза от положения рав­новесия ф_шах будет равен

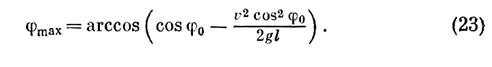
Колебания груза при неподвижной точке подвеса и постоянной длине каната

Колебания груза в плоскости Р (см. рис. 106) отличаются от колебаний груза, подвешенного на одном канате [выражение (14)], только тем, что радиусом колебаний будет не длина каната l, а ее проекция на плоскость Р, т. е. величина l_P = l cos φ₀, что и следует учесть в уравнении (14). При колеба­ниях груза в плоскости бифиляра будут наблюдаться два совершенно различных явления. Остановимся на этих явлениях и рассмотрим их более подробно.

Пусть, например, вследствие вне­запного прекращения поворота кра­на груз выйдет из положения ста­тического равновесия и начнет дви­жение влево (по рис. 106 и 107), как это было установлено выше, со скоростью v cos φ0 до положения, определяемого углом ф_maх, рассчиты­ваемым по выражению (23). Ветвь бифиляра ОБ будет при этом натяну­той, а ветвь О₁Б прослабленной. До­стигнув указанного положения, груз устремится к положению ста­тического равновесия, отмеченному на рис. 107 точкой Δ. Пренебре­гая потерями, будем считать, что груз возвращается в точку В с той же скоростью v cos φ ₀, с которой он начал движение влево из этой точки. Движение груза влево и обратно представляет собой обычные колебания, описываемые уравнением (14), происходящие относительно центра О при следующих начальных условиях:

t = 0, φ=φ_о, φ = φ₀ = vcosφ₀/2. В момент прихода груза в точку

В левая ветвь бифиляра О₁В резко натягивается, а груз «стремит­ся» продолжать движение по дуге окружности радиусом l и с цент­ром в точке О. Левая ветвь О₁В исключает возможность такого движения, в результате чего груз резко меняет направление своей скорости (с v cos φ_о на v₁), т. е. переходит на новую траекторию с тем же радиусом l, но с новым центром О₁. Это явление носит характер удара, направленного в левую ветвь каната О₁В и

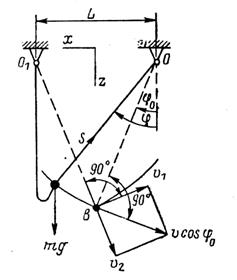
Рис. 107. Колебания груза при бифилярном подвесе.

обусловленного составляющей скорости v₂ (см. рис. 107). Если счи­тать канат абсолютно неупругим, кинетическая энергия

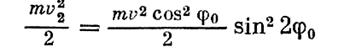
будет затрачена на неупругую деформацию каната. Кинетическая энергия

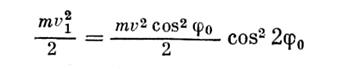
обусловливает движение груза вправо по окружности радиусом l (деформацией каната пренебрегаем) с центром в точке Ох. Это движение, естественно, также будет описываться уравнением (14), но с новыми начальными условиями: .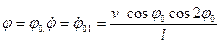

Очевидно, что при принятом допущении об абсолютной неупру­гости каната величину, получаемую из отношения

можно считать коэффициентом восстановления при ударе в канат. Из этого следует, что величину

можно назвать противораскачивающей способностью бифилярного подвеса. При φ₀ = 0 противораскачивающая способность р также равна нулю, при φ=45° р = 100%.

Таким образом, колебания груза в плоскости бифиляра носят скачкообразный затухающий характер. Собственно колебания описываются уравнением (14). В процессе колебаний канат счи­тается идеальной связью, т. е. абсолютно жестким. Решая уравне­ние (14), необходимо следить за положением груза, т. е. за углом ср. Когда текущее значение угла ср станет равным значению φ₀, расчет приостанавливается и в уравнение (14) вводятся новые начальные условия:

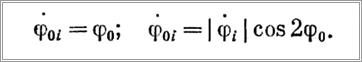
После этого расчет по уравнению (14) возобновляется и т. д. При такой методике расчета углы φ будут получаться всегда положи­тельными вне зависимости от направления колебаний.

В момент удара канат считается абсолютно неупругим. Натяже­ние в канате при ударе можно определить, используя теорему об изменении кинетической энергии, согласно которой

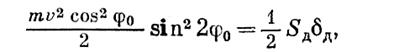
где S_д — величина динамического натяжения каната; δ _Д = S_д/с - динамическая деформация (удлинение) каната; с — жесткость каната.

После преобразований получим

Колебания груза при неподвижных точках подвеса и переменной длине ветвей канатов

Колебания груза в плоскости Р (см. рис. 106) будут описы­ваться уравнениями:

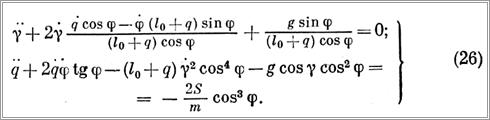
Уравнения (26) имеют единые начальные условия (см. § 41), решение их непрерывно. Для решения системы уравнений (26) необходимо иметь третье уравнение, выражающее закон изменения во времени угла φ

Колебания в плоскости бифиляра будут описываться уравне­ниями (15), но решение их будет прерывно, т. ё. с вводом новых начальных условий каждый раз при переходе грузом положения статического равновесия. Поэтому в процессе решений уравнений (15) необходимо следить за углом φ_i и, когда он достигнет значе­ния φ_0i-, определяемого формулой

необходимо в уравнение (15) ввести новые начальные условия (L — расстояние между точками подвеса; см. рис. 107): φ_оi — по формуле (28) и

Величину натяжения каната в момент перехода грузом поло­жения статического равновесия можно определить по формуле

Колебания груза при периодических перемещениях точек подвеса и переменной длине ветвей канатов

В общем случае колебания груза будут описываться уравне­ниями (18). Параллельно с решением Системы уравнений (18) необходимо вести вычисление угла φ _0i по формуле (28) и, когда текущее значение угла φ_i, определяемое путем решения системы (18), станет равным φ_0i, в систему (18) надо будет ввести новые начальные условия, определяемые по формулам (28) и (29).

Если рассматривать раздельно продольную и поперечную качки, считая при этом, например, что стрела крана занимает траверзное положение по отношению к судну, то закон колебаний груза будет выражаться следующим образом: при продольной качке — уравнениями (19), при поперечной качке — уравнениями

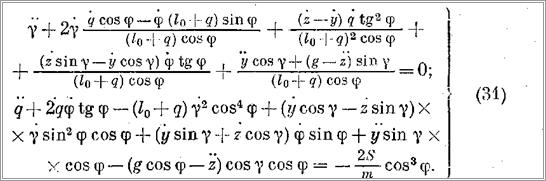
Расчет колебаний при продольной качке судна, выполняемый по уравнениям (19), следует производить параллельно с расчетом угла φ_oi по формуле (28), т. е. с периодическим введением новых начальных условий по формулам (28) и (29). Расчет колебаний при поперечной качке по уравнениям (31) производится непре­рывно с едиными начальными условиями, но совместно с реше­нием уравнения (27), выражающего закон изменения во времени угла φ. Если скорость механизма подъема крана v„ постоянна, то q = v_m, q= v_Mt. В этом случае первые уравнения систем (19), (26) и (31) становятся независимыми от вторых.

Указанная методика применима для схем устройств, приведен­ных в гл. II (см. рис. 19 и 20).