Принимающее судно; 2 - передающее судно; 3 - кранцы; 4 — креплениекранцев. 9 глава

Решение. Начало отсчета помещаем в точку О. Находим сумму проекций всех сил, действующих на тележку, на ось х

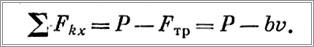
Используя уравнения (2), получим

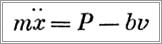
или

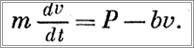
Разделяем переменные и интегрируем, учитывая начальные условия

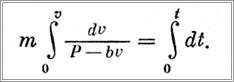
После интегрирования получим

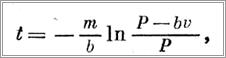
откуда

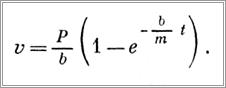
Для нахождения закона движения тележки представим послед­нее выражение в виде:

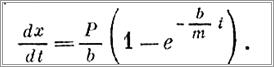
Разделяем переменные и интегрируем, учитывая начальные усло-

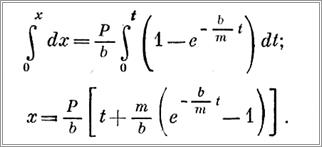
Пример 5. В условиях примера 3 определить закон колеба­ний груза, вызванных горизонтальными периодическими переме­щениями точки подвеса О, происходящими по закону х₀=asinkt (кинематическое возбуждение).

Решение. Здесь в сумму моментов действующих на груз сил относительно точки О необходимо включить переносную силу инерции F_e=|mх₀|=mак²sinkt (при х₀>0 и 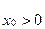перенос­ное ускорение 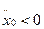, т. е. F_e создает положительный момент)

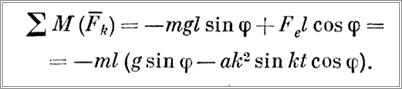
Подставляя значение (F_k) в уравнение (3) и произведя ряд преобразований, получим дифференциальное уравнение колеба­ний груза

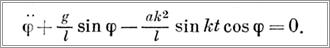
Это уравнение может быть решено одним из приближенных чис­ленных методов вручную или на ЭВМ. Приближенное аналитиче­ское решение можно получить, полагая колебания малыми, т. е. принимая sin_φ≈φ, cos_φ=1. Тогда уравнение примет вид:

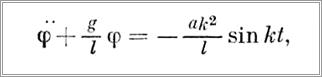
а его решением будет следующее выражение:

Постоянные интегрирования определяются исходя из началь­ных условий, которых может быть (при t = 0) четыре:

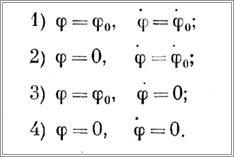
Пример 6. Определить закон движения тела 4, поднимаемого с помощью механизма, представленного на рис. 100, а, под дей­ствием постоянного момента, приложенного к телу 1.

Решение. В данном примере имеем механическую систему, состоящую из четырех тел. Применим метод разделения системы на отдельные тела (рис. 100, б) и составления дифференциальных уравнений для каждого из них в отдельности (для тел 2 и 3 составим общее уравнение). Получим четыре уравнения (движение тела 4 разбиваем на вращательное и поступательное вдоль оси z)

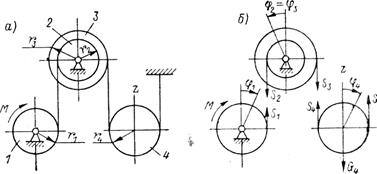
Рис. 100. К примерам 6, 12.

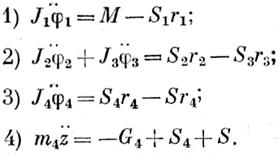
Очевидно, что S₁ = S₂ = S₁₂, S₃ = S₄ = S₃₄. Найдем взаи­мосвязь между перемещениями всех тел (взаимосвязь между скоростями и ускорениями будет тождественной), для чего сооб­щим телу 1 малое перемещение φ₁. Остальные тела получат соот­ветственно также малые перемещения φ₂=φ₃=φ₂₃, φ₄ и z₄ =z. После несложных вычислений будем иметь

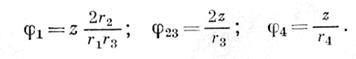
Решая совместно дифференциальные уравнения относительно z с учетом взаимосвязи между перемещениями (ускорениями), получим

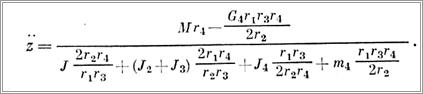
Поскольку правая часть полученного выражения содержит только постоянные величины, можно сделать вывод, что тело 4 движется равноускоренно с ускорением z.

Дифференциальные уравнения (1)—(3) позволяют произвести полный анализ изучаемого движения тела (системы тел). Однако в инженерной практике очень часто бывает достаточным знать не все характеристики движения, а только его отдельные эле­менты. Такие задачи позволяют решать так называемые общие теоремы динамики. Рассмотрим две такие теоремы, наиболее часто используемые в инженерных расчетах.

Теорема об изменении количества движения. Изменение количества движения системы (точки) за некоторый промежуток времени равно геометрической сумме импульсов всех действу­ющих на систему (точку) внешних сил за тот же промежуток времени.

Математически эта теорема записывается так:

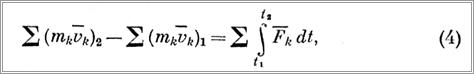
где m_k — масса k-й точки; 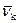— скорость k-й точки; 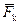— сила; индексы 1 и 2 — обозначение моментов времени, соответствующих t₁ и t₂.

При решении практических задач удобнее пользоваться урав­нениями в проекциях

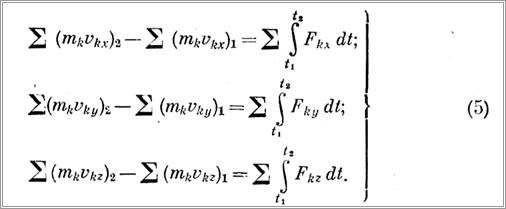
Теоремой об изменении количества движения обычно поль­зуются, когда:

— в число известных и искомых величин входят силы, время, начальная и конечная скорость, т. е. F, t, v₁, v₂;

— действующие силы постоянны или зависят только от вре­мени.

Теоремой удобно пользоваться при изучении движения среды: (жидкости, газа).

Теорема об изменении кинетической энергии. Изменение кине­тической энергии системы (точки) при некотором ее перемещении

равно алгебраической сумме работ на этом перемещении всех приложенных к системе (точке) внешних и внутренних сил. Математическая запись теоремы выглядит так:

где Т₁, T₂ — кинетическая энергия системы (точки) в соответст­вующих положениях; ∑А_к — суммарная работа всех сил на пере­мещении из второго положения в первое.

Кинетическая энергия вычисляется следующим образом:

где m — масса точки; v — абсолютная скорость точки; М — мас­са тела; v_c — абсолютная скорость центра масс; J_c — момент инерции массы тела относительно оси, проходящей через центр масс и параллельной оси вращения тела; ω — угловая скорость вращения тела.

При вычислении работ следует иметь в виду, что работу на дан­ном перемещении производит только та часть силы, которая дей­ствует вдоль направления этого перемещения, другими словами, которая определяет изменение модуля скорости рассматриваемого тела или точки.

С помощью теоремы об изменении кинетической энергии удобно решать задачи, в которых:

— в число данных и искомых величин входят силы, перемеще­ния тел (точки), начальные и конечные скорости, т. е. F, s, v₁, v₂;

— действующие силы постоянны или зависят только от рас­стояния.

Совместное применение рассмотренных теорем позволяет ре­шать более сложные задачи, в которых неизвестными (или задан­ными) являются и время движения, и перемещения точки (тел).

Порядок решения задач с помощью любой из этих двух теорем следующий.

1. Изобразить на чертеже систему (точку) в произвольном положении и обозначить все действующие на нее внешние силы (активные и реакция связей) и внутренние (для изменяемых систем).

2. Вычислить правые части уравнений (5) или (6) за время движения (импульсы) или для рассматриваемых перемещений (работы).

3. Пользуясь формулами (5), (6), составить соответствующие уравнения и вычислить искомые величины.

Заметим, что обе рассмотренные теоремы непосредственно свя­заны с основным законом динамики и из него вытекают.

Пример 7. В момент времени t₁ тележка (см. рис. 97) имела скорость v₁ Определить, через сколько времени t тележка остано­вится под действием постоянной силы трения F_Tp.

Решение. Очевидно, что для решения задачи удобно при­менить теорему об изменении количества движения. Пусть моменту времени t₁ соответствует точка О. На тележку действуют сила тя­жести G, реакция плоскости качения N и сила трения F_Tp. Напра­вляя ось Ох в сторону движения и применяя первое уравнение из системы (5), запишем

Поскольку v_lx = v_x, a v_2x = 0 (по условию), то получим

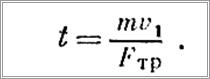
Пример 8. В положении статического равновесия грузу мас­сой т, подвешенному в точке О на канате длиною I (рис. 101), сообщили скорость v₀. Определить величину угла максимального отклонения груза от положения равновесия φ_maх. Решение. Воспользуемся теоремой об изменении кинети­ческой энергии. В произвольном положении М на груз действуют следующие силы: сила тяжести mg и сила натяжения каната S. Работа силы тяжести А=—mgh, работа же усилия S равна нулю, так как она перпендикулярна направлению перемещения (т. е. касательной к окружности). Тогда, используя уравнение (6), получим

Учитывая, что v₂=0, v₁-v₀,a h=l(1-cosφ_mах), найдем

Пример 9. Двигаясь равномерно и прямолинейно со скоро­стью v, тележка внезапно останавливается. Исходя из условия прочности определить профиль трубы, заделанной в корпусе тележки (рис. 102), к которой жестко крепится груз массой m (на­пример, посредством штыря, входящего плотно в трубу и связан­ного с механизмом подъема).

Решение. Из условия жесткости трубы примем величину допускаемого прогиба трубы, т. е. величину перемещения массы т в направлении оси х, равной

x_д=0,003l

Для решения задачи воспользуемся теоремой об изменении кинетической энергии.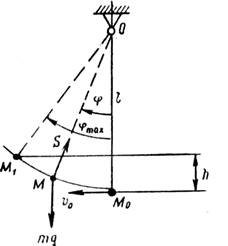

Рис. 101. К примеру 8.

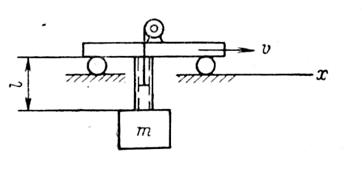
Рис. 102. К примеру 9.

Очевидно, что после остановки тележки сообщенная массе кинетическая энергия будет погашена силой упругости трубы Р. Работа силы упругости при отклонении от положения равновесия

Используя уравнение (6), получим

Учитывая, что произведение Рl представляет собой максималь­ный изгибающий момент М_и, а последний, в свою очередь, может быть выражен в виде

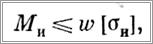
где ω — момент сопротивления поперечного сечения трубы изги­бу, а [σ_и] — допускаемое напряжение на изгиб, найдем

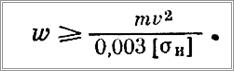
Пример 10. В условиях примера 7 определить пройденный тележкой путь.

Решение. Применяя теорему об изменении кинетической энергии, т. е. уравнение (6), получим

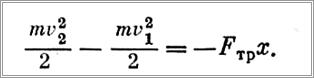
Так как по условию задачи v₂=0, то пройденный путь будет равен

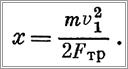
Универсальный метод решения задач динамики

Универсальный метод основан на использовании уравнений Лагранжа второго рода, которые имеют вид:

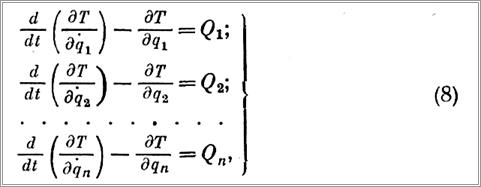
где Т — кинетическая энергия системы (точки); q_i — обобщен­ная координата; Q_i — обобщенная сила, соответствующая своей обобщенной координате; n — число обобщенных координат (равно числу уравнений); д — символ частной производной.

Обобщенными координатами называются независимые между собой параметры любой размерности (см, см², радианы и т. п.), однозначно определяющие положение системы (точки) в простран­стве. Число обобщенных координат всегда равно числу степеней свободы системы (точки).

Число степеней свободы для системы с геометрическими свя­зями (число обобщенных координат)

n=3s—к,

где s — число материальных тел (точек), входящих в систему; к — число уравнений связей.

Обобщенные силы — это коэффициенты при приращениях обоб­щенных координат, сумма произведений которых (коэффициентов на соответствующее приращение) дает выражение для полной эле­ментарной работы действующих на систему сил (при идеальных связях только активных сил). Очевидно, что размерность обоб­щенной силы равна размерности работы, деленной на размерность соответствующей обобщенной координаты.

Вычисление кинетической энергии. Кинетическая энергия си­стемы (точки) вычисляется по формулам (7), При вычислении ки­нетической энергии отдельных точек прежде всего необходимо найти выражение для абсолютной скорости точки. При этом если точка совершает сложное движение, удобно скорости всех состав­ных движений точки спроецировать на оси декартовой системы координат и вычислять абсолютную скорость по формуле

где v_x, v_y, v_z — суммы проекций составных скоростей на коор­динате оси х, y, z.

Вычисление обобщенных сил. Выражения для обобщенных сил находятся по формулам вида:

где δ q_i — элементарное приращение обобщенной координаты при сообщении системе независимого возможного перемещения по этой координате, при котором все остальные обобщенные коорди­наты не изменяются; δ А_i — сумма элементарных работ всех действующих сил на рассматриваемом перемещении.

Сначала системе сообщается такое независимое возможное перемещение, при котором приращение получает только одна координата, например q₁, а остальные не изменяются. Во избежание ошибок в знаках возможное перемещение необходимо направлять так, чтобы приращение соответствующей координаты было бы положительным. Вычисляется работа всех действующих сил, например , А, на рассматриваемом перемещении δ q₁. По формуле (10) находится выражение для обобщенной силы. Затем даем систе­ме другое возможное перемещение (по координате q₂) и находим δ А₂ и т. д.

Общий порядок решения задач методом Лагранжа. Решение задач методом Лагранжа производится в следующем порядке.

1. Устанавливается число степеней свободы системы и выби­раются обобщенные координаты.

2. Система изображается в произвольном положении, обозна­чаются все действующие на систему силы (активные и силы тре­ния), если последние совершают работу.

3. Составляются выражения для обобщенных сил.

4. По формулам (7) составляется выражение для полной кине­тической энергии системы в ее абсолютном движении; предвари­тельно вычисляются выражения для абсолютной скорости отдель­ных точек или тел через обобщенные координаты.

5. Вычисляются соответствующие производные от кинетиче­ской энергии и подставляются вместе с выражениями для обоб­щенных сил в формулы (8).

Результаты вычислений по уравнениям Лагранжа (8) в конеч­ном итоге приводят к тем же дифференциальным уравнениям, составляемым по формулам (1)—(3), т. е. уравнения (8) предста­вляют собой обыкновенные дифференциальные уравнения второго порядка относительно обобщенных координат q₁ q₂, . . ., q_n.

Преимущество и универсальность уравнений Лагранжа за­ключаются в следующем.

1. Если уравнения (1)—(3) справедливы только в инерциальной системе отсчета, то уравнения Лагранжа справедливы и в неинерциальной системе.

2. Вид и число уравнений Лагранжа не зависят ни от количе­ства тел (точек), входящих в рассматриваемую систему, ни от вида движения, т. е. уравнения справедливы как для абсолютного, так и для относительного движения. В них отсутствуют силы инер­ции, вычисление которых связано с известными трудностями. Последнее обстоятельство исключает необходимость вычисления ускорений переносного и кориолисова.

3. При идеальных связях в правые части уравнений входят только активные обобщенные силы, что позволяет исключить из рассмотрения все заранее неизвестные реакции связей.

Пример 11. По условиям примера 5, пользуясь методом Ла­гранжа, определить закон колебаний груза (см. рис. 99).

Решение. Система имеет одну степень свободы. В качестве обобщенной координаты выбираем угол ср. Считая канат идеальной связью (как и в примере 5), будем иметь только одну активную силу — силу тяжести mg. Сообщим грузу элементарное переме­щение по обобщенной координате φ, т. е. отклоним груз от произ­вольного положения От на угол δ φ против часовой стрелки (т. е. в положительном направлении). Перемещение груза при этом вы­разится длиной дуги l δ φ. Работу на этом перемещении будет про­изводить составляющая массы груза, спроецированная на каса­тельную к дуге, т. е. mg sin φ,

Работа отрицательна, так как сила mg sin φ направлена в сторону, противоположную перемещению δ φ. По формуле (10) найдем обобщенную силу, соответствующую обобщенной координате φ,

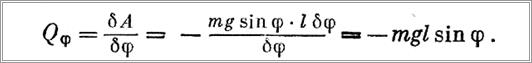
Для вычисления абсолютной скорости груза найдем проекции всех скоростей на оси х, у

Тогда квадрат абсолютной скорости груза будет

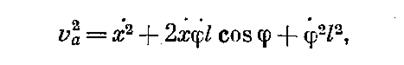
а кинетическая энергия груза в абсолютном движении

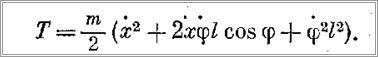
Подставляя значения Q_2φ и Т в формулу (8) и произведя ряд преобразований, получим дифференциальное уравнение колебаний груза, аналогичное полученному в примере 5.

Пример 12. Решить задачу по условиям примера 6 (см. рис. 100) методом Лагранжа.

Решение. Система имеет одну степень свободы, так как перемещения всех тел взаимосвязаны (отсутствуют независимые перемещения тел) и могут быть охарактеризованы через перемещение любого из них. Выберем в качестве обобщенной координаты угол φ₁, характеризующий вращение тела 1. Зависимость между перемещениями φ₁,φ₂, φ₃,φ₄ и z установлена в примере 6. Сообщим телу 1 элементарное перемещение δ φ₁ в направлении движения, т. е. по часовой стрелке. Тогда тела ,2 и 3 повернутся на угол 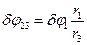, тело 4 повернется на угол 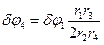и поднимется вдоль оси z на расстояние 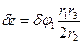. Работу на этих перемещениях будут совершать только активные силы М и G, т. е.

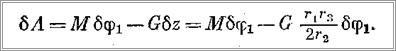
Обобщенная сила по формуле (10) будет

Кинетическая энергия системы

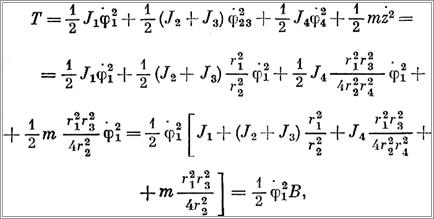
Найдем производные от кинетической энергии в соответствии с формулой (8)

Подставляя полученные значения производных и обобщенной силы в формулу (8), найдем

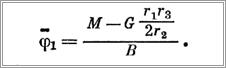
Решая последнее выражение относительно 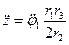получим тот же результат, что и в примере 6.

§ 41. Динамика груза, подвешенного к крану на одном канате

В данном параграфе рассматриваются схемы устройств переда­чи грузов контактным способом (см. гл. II, рис. 15, 17 и др.).

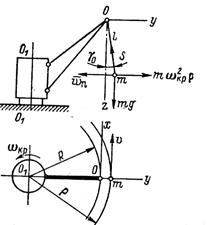
Рис. 103. Равномерный поворот крана.

Равномерный поворот крана при постоянном вылете стрелы

При повороте крана с постоянной угловой скоростью ω_кр на груз массой т будут действовать следующие силы (рис. 103): сила тяжести mg, натяжение каната S и центробежная сила инерции mω_kp обусловленная нормальным ускорением w_n=ω. Центробежная сила инерции вызывает отклонение груза от вертикали на угол у₀, вследствие чего траекторией движения груза будет дуга окружности радиусом р, в то время как точка подвеса О пе­ремещается по дуге радиу­сом R. Из условия равновесия груза найдем величину угла у₀, для чего спроецируем все дей­ствующие на груз силы на ко­ординатные оси у и z

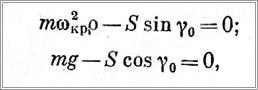
откуда найдем

С другой стороны,

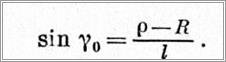
Учитывая малые угловые скорости кранов, т. е. заранее пола­гая углы у₀ малыми (например, не более 10°), можно считать, что sin у₀ ≈ tg y₀ и тогда

откуда

Поскольку мы ограничились рассмотрением малых углов (до 10°), то уравнение (12) будет справедливым при соблюдении сле­дующего условия:

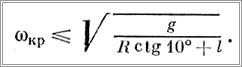
Точное определение угла у₀ осложняется вследствие того, что совместное решение исходных уравнений приводит к алгебраиче­скому уравнению, содержащему при неизвестном у₀ все степени от первой до четвертой.

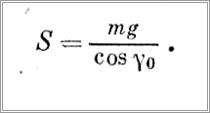
Натяжение каната можно определить по формуле

Внезапное прекращение поворота крана

При внезапной остановке крана груз будет «стремиться» продолжать движение в направлении линейной скорости v = ω_крр, которую он имел перед остановкой (см. рис. 103). С дру­гой стороны, после остановки крана исчезнет центробежная сила инерции, поскольку теперь ω_кр = 0 и w_n = 0. Следовательно, груз начнет двигаться и в сторону уменьшения угла у₀, стремясь занять устойчивое положение равновесия, т. е. стремясь к отвес­ному положению (в первом же движении груз уходит от него). Совершенно очевидно, что как первое, так и второе движение будет носить колебательный характер. Вопросы, относящиеся к колеба­ниям, будут рассмотрены ниже. Здесь же, пренебрегая величиной угла у₀ (считая, что он равен нулю) и колебательным процессом, определим величину максимального отклонения груза от вер­тикали в сторону скорости v после внезапной остановки крана. Применим для этого теорему об изменении кинетической энергии.

В момент остановки крана груз имел кинетическую энергию mv²/2. Поскольку нас интересует максимальное отклонение груза (обо­значим его через φ_mах), то скорость груза при достижении φ_шах станет равной нулю, т. е. вся кинетическая энергия груза будет затрачена на его подъем на высоту h = l (1 — соsφ_mах). Отсюда получим

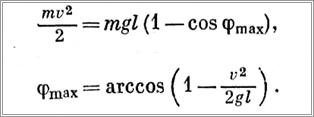
Колебания груза при неподвижной точке подвеса и постоянной длине каната (свободные колебания)

Причинами колебаний груза могут быть:

— отклонение груза от вертикали на угол φ₀;

— сообщение грузу начальной скорости φ₀;

— совместное действие первых двух факторов. Рассмотрим, как будут происходить колебания груза после внезапной остановки крана (см. рис. 103). Применим для этого ме­тод Лагранжа. В данном случае груз имеет две степени свободы, поскольку колебания происходят не в плоскости, а в пространстве и одной координатой охарактеризовать положение груза невоз­можно. В качестве обобщенных координат выберем угол у, харак­теризующий положение плоскости Р, проходящей через канат и параллельной оси Ох, и угол φ (на рисунке не показан), харак­теризующий отклонение каната в плоскости Р от линии пересече­ния плоскостей Р и Oyz (система отсчета Oxyz неподвижна). Обобщенные силы запишутся в следующем виде:

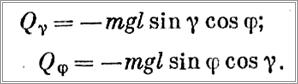
Проекции скоростей на декартовы координатные оси

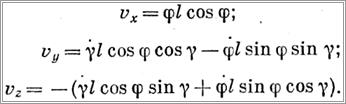
Подставляя значения проекций скоростей и обобщенных сил в формулы (7), (8), (9) и произведя соответствующие преобразова­ния, получим следующую систему дифференциальных уравнений колебаний груза:

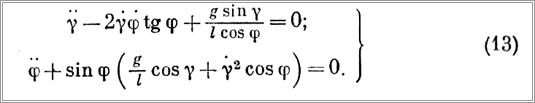
Данная система уравнений может быть решена одним из при­ближенных методов вручную или на ЭВМ. Начальными условиями будут (при t = 0): φ₀ = 0, φ₀ = v/l, у₀ — по формуле (12), у₀ = 0.

Чтобы получить дифференциальное уравнение плоских колеба­ний, необходимо в первом уравнении системы (13) принять φ и его производные равными нулю или, наоборот, во втором уравнении принять равными нулю у и его производные. Тогда получим

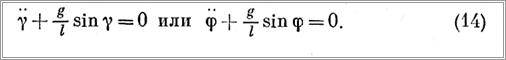
Колебания груза при неподвижной точке подвеса и переменной длине каната

Рассмотрим колебания, происходящие в одной плоскости (рис. 104). Причины колебаний остаются теми же, что и при сво­бодных колебаниях. В данном случае груз также имеет две степени

свободы. В качестве обобщенных ко­ординат примем: угол φ и удлинение каната q (считаем, что груз опу­скается).

Обобщенными силами будут

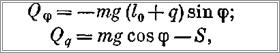
а квадрат абсолютной скорости

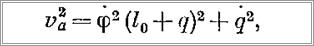
где l₀ — длина каната при t = 0.

Используя полученные выражения и формулы (7)—(9), получим систему дифференциальных уравнений колеба­ний груза

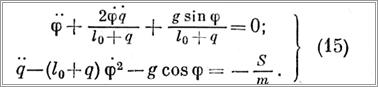
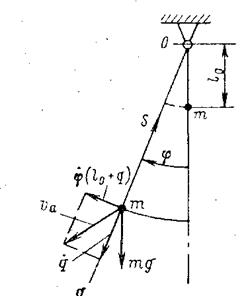
Рис. 104. Колебания при переменной длине каната.

Если груз опускается (поднимается) с постоянной скоростью v_M, т. е. q = v_m то первое уравнение системы (14) становится независимым от второго уравнения (поскольку закон изменения q известен). Первое уравнение системы (15) примет при этом вид:

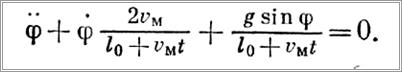
Второе уравнение (после решения первого) позволит определить закон изменения во времени натяжения каната S (при q = v_m = const, q = 0)

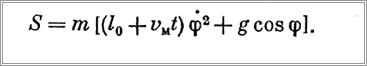
Колебания груза при периодических перемещениях точки подвеса и переменной длине каната

Будем считать, что судно, на котором установлен кран, испытывает одновременно продольную и поперечную качку, которая описывается уравнениями вида:

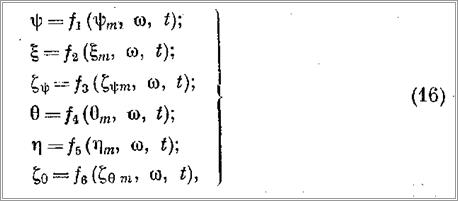
где ψ - угол дифферента (положительный при дифференте в корму); θ — угол крена (положительный при крене на левый

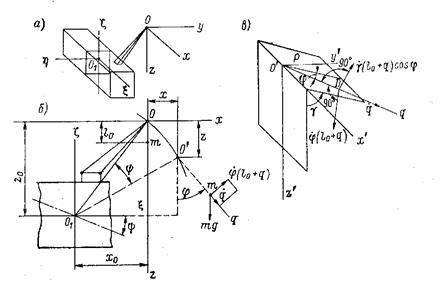
Рис. 105. Общий случай ко­лебаний.

борт); ξ — продольно-горизонтальное перемещение; η — попе­речно-горизонтальное перемещение; ξ _в —вертикальные перемещения при крене и дифференте; ψ_m, θ_m,ξ_m ,η_m — амплитуды соответствующих перемещений; φ — частота волнения моря.

Система координат 0₁ ξ η(рис. 105, а, δ) неподвижна, начало отсчета совпадает с центром тяжести судна. В точке подвеса О, соответствующей положению судна на тихой воде, поместим начало другой неподвижной системы координат Oxyz.