Поверхностный эффект в круглом проводе

Электромагнитное поле в проводящей среде в общем случае описывается системой уравнений Максвелла в комплексной форме:

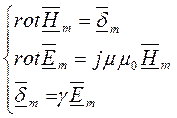
Если оси координат выбрать так, как показано на рис. 287, т.е. ось z со­вмес­тить с осью провода и положительным направлением тока, то вектор на­пря­жен­ности электрического поля 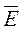будет направлен по оси z (согласно закону Ома 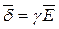), а вектор напряженности магнитного поля 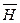будет направлен нор­мально к радиусу по правилу правоходового винта.

В цилиндрической системе координат те же уравнения примут вид:

.

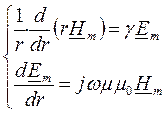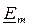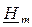Совместное решение этой системы уравнений относительно комплекс­ных перемен­ных и дает следующий результат:

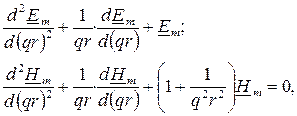
где ,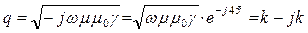

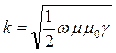
Уравнение для переменной 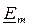представляет собой уравнение Бесселя ну­левого по­рядка при n = 0, а уравнение для переменной 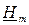– уравнение Бес­селя первого порядка при n = 1. Решения этих уравнений известны из матема­тики. Окончательные решения для векто­ров поля получают вид:

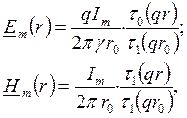
где 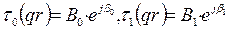– функции Бесселя соответст­венно нулевого и пер­вого по­рядка от комплексного аргумента qr и сами явля­ются комплексными числами.

Общий вид функции Бесселя n–го порядка выражается бесконечным ря­дом

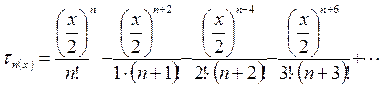
Значения функций Бесселя приводятся в математических справочниках в виде таблиц или диаграмм.

Анализ решения для вектора напряженности электрического поля 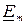и соответст­венно для вектора плотности тока 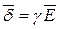показывает, что перемен­ный ток по сечению ци­линдрического провода распределяется неравномерно: его плотность d возрастает по на­правлению от центра к поверхности при­мерно по экспоненциальному закону. Эта неравно­мерность выражена тем больше, чем больше число kи радиус провода r₀ (рис. 288).

Явление возрастания плотности тока от центра к поверхности провода получило на­звание поверхностного эффекта. Поверхностный эффект возрас­тает с ростом частоты f, магнитной проницаемости m, удельной проводимости g. В технике сильных токов (на час­тоте 50 Гц) это явление сказывается незна­чи­тельно в медных и алюминиевых проводах большого сечения, и в сильной сте­пени - в сталь­ных (m>>1) проводах любого сечения.

На расстоянии D= 1/k от поверхности провода плотность тока убывает в ²е² раз, это расстояние называют глубиной проникновения поля:

.

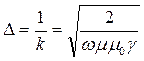Как известно, сопротивление проводника постоянному току или омиче­ское сопро­тивление определяется по формуле:

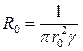[Ом/м].

Внутреннее комплексное сопротивление того же проводника перемен­ному току с учетом поверхностного эффекта может быть выражено через па­ра­метры поля:

.

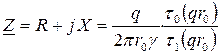Явление возрастания плотности тока от центра к поверхности провода получило на­звание поверхностного эффекта. Поверхностный эффект возрас­тает с ростом частоты f, магнитной проницаемости m, удельной проводимости g. В технике сильных токов (на час­тоте 50 Гц) это явление сказывается незна­чи­тельно в медных и алюминиевых проводах большого сечения, и в сильной сте­пени - в сталь­ных (m>>1) проводах любого сечения.

Практический интерес представляет отношение активного сопротивления провода к омическому R/R₀, количественно характеризующее поверхностный эффект в проводе. Рас­четы показывают, что на промышленной частоте 50 Гц увеличение активного сопротивле­ния R / R₀ незначительно для медных и а­лю­миниевых проводов (m = 1) и существенно для стальных проводов (m>>1). С ростом частоты fвследствие усиления поверхностного эф­фекта происходит увеличение активного сопротивления провода (R/R₀>1).