Т4. Переменное электромагнитное поле
1. Основные уравнения Максвелла и их физический смысл
Основы теории электромагнитного поля или электродинамики были впервые изложены в 1873 г. английским ученым Максвеллом в труде «Трактат об электричестве и магнетизме». Математические уравнения, описывающие физические процессы в переменном электромагнитном поле, называются уравнениями Максвелла. Наиболее важные из них первые четыре, которые называются основными:
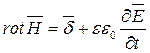 ( 1 )
( 1 )
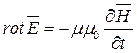 ( 2 )
( 2 )
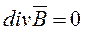 ( 3 )
( 3 )
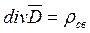 ( 4 )
( 4 )
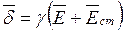 ( 5 )
( 5 )
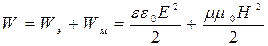 ( 6 )
( 6 )
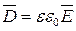 ( 7 )
( 7 )
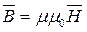 ( 8 )
( 8 )
Рассмотрим более детально каждое из уравнений Максвелла и вытекающие из них следствия.
Физический смысл 1-го основного уравнения: переменное магнитное поле ( 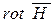 ) возбуждается как токами проводимости (
) возбуждается как токами проводимости ( 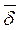 ), так и токами смещения (
), так и токами смещения ( 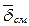 ). Максвелл назвал плотностью тока смещения изменение во времени вектора электрического смещения
). Максвелл назвал плотностью тока смещения изменение во времени вектора электрического смещения 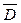 :
:
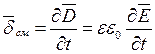
Ток проводимости ( 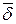 ) и ток смещения (
) и ток смещения ( 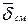 ) эквиваленты в отношении создания магнитного поля, но представляют собой различные физические явления. Если ток проводимости соответствует движению свободных зарядов, то ток смещения может существовать в пустоте, где заряды отсутствуют вообще.
) эквиваленты в отношении создания магнитного поля, но представляют собой различные физические явления. Если ток проводимости соответствует движению свободных зарядов, то ток смещения может существовать в пустоте, где заряды отсутствуют вообще.
Так как 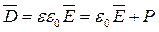 , то
, то 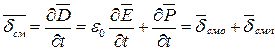
Таким образом, плотность тока смещения в диэлектрике складывается из плотности тока смещения в пустоте ( 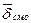 ) и члена (
) и члена ( 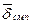 ), учитывающего поляризацию диэлектрика (перемещение связанных зарядов).
), учитывающего поляризацию диэлектрика (перемещение связанных зарядов).
1-е уравнение Максвелла представляет собой дифференциальную форму обобщенного закона полного тока. Для доказательства этого положения проинтегрируем обе части уравнения по некоторой неподвижной поверхности S, опирающейся на контур l:
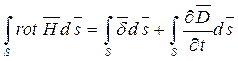
Левая часть уравнения преобразуется по теореме Стокса: 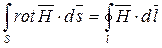 , а в правой части равенства получим:
, а в правой части равенства получим: 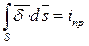 ,
, 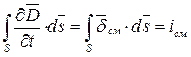 , следовательно:
, следовательно:
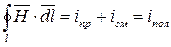 - закон полного тока в интегральной форме.
- закон полного тока в интегральной форме.
Для стационарного поля 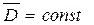 и
и 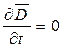 , тогда первое уравнение Максвелла превращается в уравнения магнитного поля постоянного тока:
, тогда первое уравнение Максвелла превращается в уравнения магнитного поля постоянного тока:
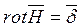 ,
, 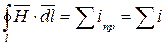 .
.
Из последнего равенства вытекают уравнения 2-го закона Кирхгофа для магнитной цепи:
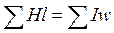 .
.
Возьмем операцию div от левой и правой части основного уравнения (1):
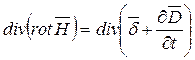
Из математики известно, что div rot = 0 тождественно, тогда получим:
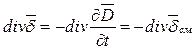 - уравнение непрерывности линий вектора плотности тока
- уравнение непрерывности линий вектора плотности тока 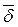 , которое гласит, что линии вектора
, которое гласит, что линии вектора 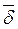 непрерывны, концами линий плотности тока проводимости
непрерывны, концами линий плотности тока проводимости 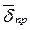 являются начала линий плотности тока смещения
являются начала линий плотности тока смещения 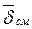 и наоборот.
и наоборот.
Проинтегрируем обе части последнего уравнения по некоторому замкнутому объему V. В левой части по теореме Остроградского получим:
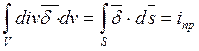 ,
,
а в правой части:
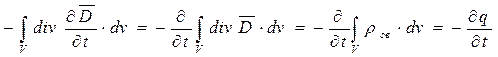 ,
,
следовательно: 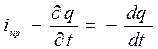 – закон сохранения заряда в интегральной форме.
– закон сохранения заряда в интегральной форме.
Полученное уравнение показывает, что в переменном электромагнитном поле токи и заряды связаны и не могут задаваться независимо друг от друга.
Физический смысл 2-го основного уравнения: переменное электрическое поле ( 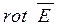 ) возбуждается не только зарядами q, но и изменением во времени магнитного поля (
) возбуждается не только зарядами q, но и изменением во времени магнитного поля ( 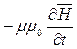 ).
).
2-е уравнение Максвелла представляет собой дифференциальную форму закона электромагнитной индукции. Для доказательства этого положения проинтегрируем обе части уравнения по некоторой неподвижной поверхности S, опирающейся на контур l:
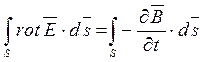 .
.
Левая часть уравнения преобразуется по теореме Стокса: 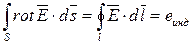 , а в правой части равенства получим:
, а в правой части равенства получим: 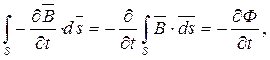 следовательно:
следовательно:
|
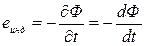
В электрических машинах переменного тока (генераторах, двигателях, трансформаторах) магнитное поле изменяется во времени по синусоидальному закону 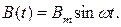 В обмотках машин это поле наводит синусоидальную ЭДС:
В обмотках машин это поле наводит синусоидальную ЭДС:
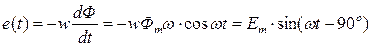 .
.
Действующее значение этой ЭДС равно:
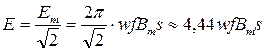 - уравнение трансформаторной ЭДС.
- уравнение трансформаторной ЭДС.
Для стационарного поля 
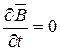 , и 2-е уравнение Максвелла превращается в уравнения электростатического поля:
, и 2-е уравнение Максвелла превращается в уравнения электростатического поля: 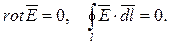
Из совместного анализа 1-го и 2-го уравнений Максвелла следует вывод, переменное электрическое и переменное магнитное поля должны рассматриваться как два связанных проявления единого электромагнитного процесса. Каждое из этих полей и их изменения во времени и пространстве являются одновременно и причиной и следствием друг друга. Совокупность этих двух полей называется электромагнитным полем.
3-е уравнение Максвелла 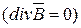 устанавливает истоки линий магнитного поля. Оно гласит, что линии вектора магнитной индукции
устанавливает истоки линий магнитного поля. Оно гласит, что линии вектора магнитной индукции 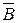 непрерывны, т.е. замкнуты сами на себя. Проинтегрируем это уравнение по некоторому объему V, ограниченному поверхностью S:
непрерывны, т.е. замкнуты сами на себя. Проинтегрируем это уравнение по некоторому объему V, ограниченному поверхностью S:
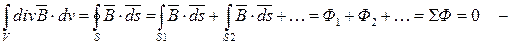
есть 1-й закон Кирхгофа для магнитной цепи.
4-е уравнение Максвелла 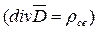 устанавливает истоки линий электрического поля. Оно гласит, что линии вектора электростатической индукции
устанавливает истоки линий электрического поля. Оно гласит, что линии вектора электростатической индукции 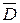 имеют разрыв, они начинаются на положительных зарядах и заканчиваются на отрицательных. Проинтегрируем это уравнение по некоторому объему V, ограниченному поверхностью S:
имеют разрыв, они начинаются на положительных зарядах и заканчиваются на отрицательных. Проинтегрируем это уравнение по некоторому объему V, ограниченному поверхностью S:
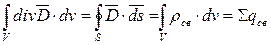 или
или 
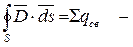
есть уравнение теоремы Гаусса в интегральной форме.
Дата добавления: 2020-07-18; просмотров: 732;











