Плоская гармоническая волна в проводящей среде

Пусть плоская гармоническая волна проникает в проводящую среду 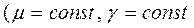) через плоскость, нормальную и направленную движе­ния волны.

Система уравнений Максвелла в комплексной форме будет иметь вид:

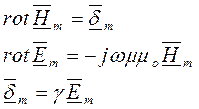
Плотностью тока смещения ( 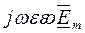) в уравнении (1) пренебрегаем в связи с ее малостью по сравнению с плотностью тока проводимости .

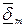Выберем направления осей координат так, чтобы вектор 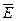сопадал с осью x ( 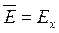), вектор 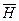совпадал с осью y ( 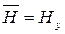), тогда вектор Пойтинга 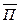будет направлен по оси z ( 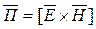) (рис. 284). При таком выборе направле­ний осей координат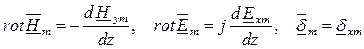 и система уравнений Максвелла получит вид:

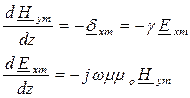
Решим данную систему дифференциальных уравнений относительно од­ной из пере­менных, например, 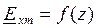. Для этой цели продифференцируем уравнение (2) по пере­менной (z) и сделаем в него подстановку из уравнения (1):

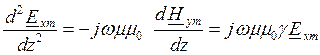
Введем обозначения:

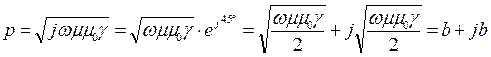, где .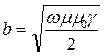

С учетом принятых обозначений дифференциальное уравнение получит стандартную форму:

.

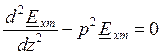Решение дифференциального уравнения:

,

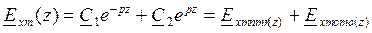где a₁= -p = -b – jb, a₂ = b+jb - корни характеристического уравнения.

Если среда распространения волны не ограничена, то отраженная волна отсутствует и второе слагаемое из решения можно исключить, тогда решение в комплексной форме по­лучит вид:

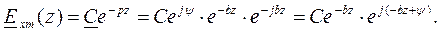
Перейдем от комплексного изображения к функции времени:

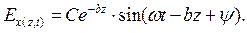
Решение для волны 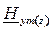в комплексной форме получим из уравнения (2) путем подстановки в него найденного решения для :

,

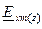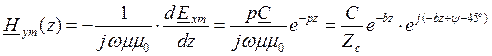где 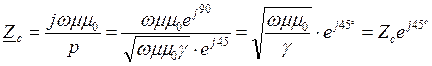-комплексное волно­вое сопро­тивле­ние среды, которое носит активно-индуктивный характер.

Перейдем от комплексного изображения к функции времени:

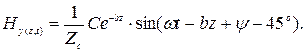
Таким образом, электромагнитное поле в проводящей среде распростра­няется в виде затухающих взаимно перпендикулярных волн и . Множитель 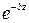показывает, что амплитуды волн при своем перемещении зату­хают по экспоненциальному закону. Глу­биной проникновения поля называется расстояние, на котором амплитуды волн затухают в 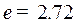раза, т.е 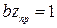, от­куда .

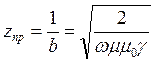Фазовая скорость определяется из условия, что 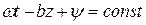, откуда следует, что .

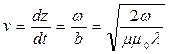Длина волны l равна расстоянию, на котором фаза волны изменяется на 2p, т. е. 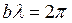, откуда 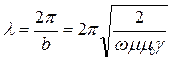. На расстоянии длины волны z =l зату­хание волны составит 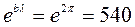раз.