Т4. Переходные процессы в нелинейных цепях

Общая характеристика переходных процессов в нелинейных цепях

Переходные процессы в нелинейных цепях описываются системой нели­нейных диф­ференциальных уравнений, составленных для схемы цепи по зако­нам Кирхгофа. Расчет пере­ходных процессов в нелинейных цепях сводится, та­ким образом, к решению системы нели­нейных дифференциальных уравнений. Значительные трудности, возникающие при таких расчетах, обусловлены слож­ностью решения нелинейных дифференциальных уравнений.

Для расчета переходных процессов в нелинейных цепях нельзя указать общие методы, применимые для любого класса цепей. Выбор метода расчета всегда индивидуален и опреде­ляется конкретными условиями задачи: структу­рой схемы цепи, видом уравнения аппрокси­мации нелинейной характеристики, требованиями к форме искомой функции и др. Ниже пе­речислены наиболее важные методы, которые применяются для расчета переходных процес­сов в не­линейных цепях:

1) метод интегрируемой аппроксимации характеристики нелинейного элемента;

2) метод кусочно-линейной аппроксимации характеристики нелиней­ного элемента;

3) метод условной линеаризации нелинейного дифференциального урав­нения;

4) метод численного интегрирования системы нелинейных дифференци­альных урав­нений.

Переходные процессы в нелинейных цепях могут существенно отличаться от пере­ходных процессов в аналогичных по структуре линейных цепях. Нели­нейность характери­стики какого-либо элемента цепи может привести или только к чисто количественному изме­нению переходного процесса или к его качественным изменениям. В первом случае на неко­торых отрезках времени скорость переходного процесса увеличивается, а на других отрезках времени - замедляется. Во втором случае в цепи возникает качественно новые явления, принципиально невозможные в линейных цепях, например, незатухающие ав­токолебания с произвольной постоянной или плавающей частотой.

Расчет переходного процесса методом интегрируемой

Аппроксимации

Метод основан на аппроксимации характеристики нелинейного элемента такой функ­цией, которая позволяет проинтегрировать дифференциальное урав­нение цепи стандартным методом.

Ценность метода заключается в том, что в результате интегрирования, решение для искомой функции получается в общем виде, что позволяет иссле­довать влияние на искомую функцию различных факторов. Метод применим главным образом к простым электрическим цепям, процессы в которых описы­ваются дифференциальным уравнением 1-го порядка.

Рассмотрим применение данного метода к расчету переходного процесса при включе­нии нелинейной катушки i(y) к источнику постоянной ЭДС E(рис. 245). Вебер-амперную характеристику нелинейной катушки аппроксимируе­мым уравнением 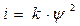.Дифференциальное уравнение цепи составляется по 2-му закону Кирхгофа: 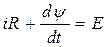, откуда следует:

,

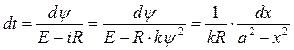где обозначены x=y, a= .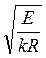

По таблице интегралов находим решение:

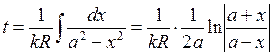
Настоящая задача имеет аналитическое решение при аппроксимации не­линейной ха­рактеристики некоторыми другими уравнениями, например i=ky³, i=ky⁴.