Расчет переходного процесса методом кусочно-линейной аппроксимации

Метод основан на аппроксимации характеристики нелинейного элемента отрезками прямой. При такой аппроксимации дифференциальные уравнения цепи на отдельных участ­ках будут линейными и могут быть решены извест­ными методами (классическим или опера­торным). При переходе от одного уча­стка к другому в дифференциальных уравнениях будут скачком изменяться по­стоянные коэффициенты, что повлечет скачкообразное изменение ко­эффициен­тов в их решении. Решения для отдельных участков сопрягаются между собой на стыках участков на основе законов коммутации.

Рассмотрим применение данного метода к расчету переходного процесса при включе­нии нелинейной катушки к источнику постоянной ЭДС Е (рис. 245а). Нелинейную вебер-ам­перную характеристику катушки y(i) заменим отрезками прямой линии (ломаной линией 0-1-2-3) (рис. 246):

Аппроксимируем отдельные отрезки ломаной линии уравнениями пря­мой:

1) для отрезка 0-1 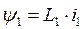, где ;

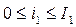2) для отрезка 1-2 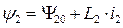, где ;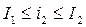

3) для отрезка 2-3 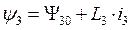, где .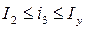

Коэффициенты аппроксимации Y₂₀, Y₃₀ определяются из графической диаграммы, а коэффициенты L₁, L₂, L₃ - через координаты точек стыка отрезков (0,1, 2, 3):

, , .

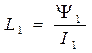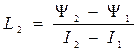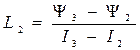Дифференциальные уравнения для отдельных участков будут иметь вид:

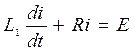, где 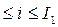0 , 0 ,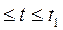

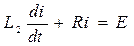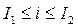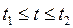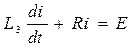, где , ,

, где ,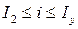

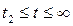
Решения уравнений для отдельных участков, найденные классическим методом, будут отличаться только постоянными коэффициентами:

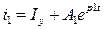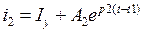1) , 2) , 3) ,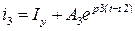

где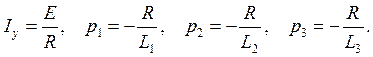

Постоянные интегрирования находятся из начальных условий и законов коммутации:

1) при t = 0, i₁(0) = 0, из решения (1) следует A₁= -I_y,

2) при t = t₁, i₂(t₁) = I₁, из решения (2) следует A₂= I₁-I_y,

3) при t = t₂, i₃(t₂) = I₂, из решения (3) следует A₃= I₂-I_y.

Моменты времени t₁, t₂, соответствующие переходу процесса с одного участка харак­теристики на другой, определяются из совместного решения урав­нений для смежных участ­ков в точке стыка:

1) для точки 1: 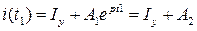, откуда следует ,

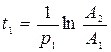2) для точки 2: 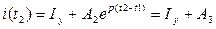, откуда следует .

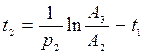Графическая диаграмма переходного процесса показана на рис. 247.Нали­чие изломов на графической диаграмме искомой функции i(t) объясняется по­грешностями аппроксимации характеристики нелинейного элемента возле точек стыка отдельных участков. Достоинство данного метода состоит в том, что он позволяет применить к расчету переходных процессов в нелинейных цепях из­вестные методы расчета переходных процессов в линейных цепях.