Расчет мгновенных значений параметров режима гармоническими методами

В нелинейных цепях переменного тока происходят искажения форм кривых токов и напряжений. Несинусоидальные функции токов i(t)и напряже­ний u(t), как известно, можно представить в виде гармонических рядов Фурье. В гармонических методах расчета решение для искомых величин находят в виде суммы отдельных гармоник.

В простейших случаях решение для искомой функции в виде гармони­ческого ряда Фурье удается получить в результате разложения в ряд Фурье най­денного в общем виде ре­шения. В качестве примера рассмотрим расчет тока в нелинейной катушке (тока холостого хода трансформатора) (рис. 241). Чтобы по­лучить сравнительно простое решение, применим для катушки параллельную схему замещения (рис. 44). Вебер-амперную характеристику ка­тушки аппрокси­мируем уравнением степенного полинома: i_L(y) = ay + by⁵.

Пусть к зажимам катушки приложено напряжение u(t)=U_m×sin(wt+90^o).Магнитное по­токосцепление катушки связано с напряжением уравнением ин­дукции:

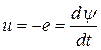, откуда .

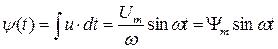Ток в резисторе определяется по закону Ома:

.

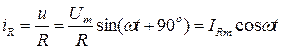Ток в катушке найдется в результате подстановки функции y(t)в уравне­ние аппрок­симации:

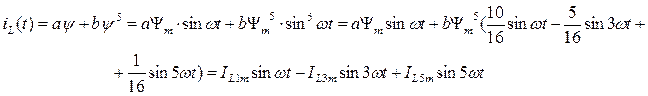
Ток источника определяется по первому закону Кирхгофа, при этом сло­жение гармо­ник токов одинаковой частоты можно выполнять в комплексной форме:

,

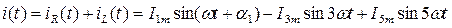где I_1m= I_L1m+ jI_R1m= I_1me^ja1.

Анализ решения показывает, что намагничивающий ток катушки имеет несинусои­дальную форму и содержит в своем составе только нечетные гармо­ники, при этом основная гармоника тока отстает от приложенного напряжения на угол j = y_u - y_i = 90^o - a₁.

Решение для искомой функции в виде суммы гармоник можно получить также мето­дом гармонического баланса. Суть этого метода состоит в том, что ожидаемое решение для функции f(t)представляется в виде суммы основной и нескольких высших гармоник:

,

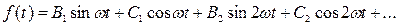где В₁, С₁, В₂, С₂…- неизвестные коэффициенты, подлежащие определению. За­тем ампли­туды гармоник всех токов и напряжений выражаются через неизвест­ные коэффици­енты. По­сле этого балансируются коэффициенты для одинако­вых гармоник в уравнениях Кирхгофа, составленных для расчетной схемы. В результате получается система алгебраиче­ских урав­нений с неизвестными ко­эффициентами искомой функции, в результате решения которой оп­ределяются сами коэффициенты.

В качестве примера рассмотрим расчет режима в схеме рис. 242.

Пусть к выводам схемы приложено синусоидальное напряжение

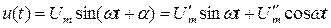, а вебер-амперная характеристика не­линей­ной катушки аппроксимирована уравнением .

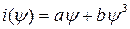Дифференциальное уравнение цепи будет иметь вид:

.

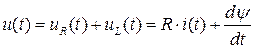В качестве неизвестной функции, подлежащей определению, принимаем потокосцеп­ление y(t), решение для которой будем искать в виде суммы 1-й и 3-й гармоник (четные гар­моники в решении отсутствуют):

,

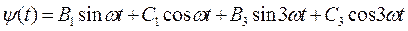где В₁, С₁, В₃, С₃ - неизвестные коэффициенты.

Выражаем ток и напряжения на отдельных участках схемы через искомую функцию y(t):

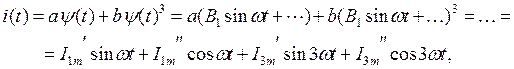
где амплитуды гармоник состоят в некоторой функциональной зависимости от неизвестных коэффициентов В₁, С₁, В₃, С₃.

.

.

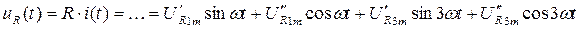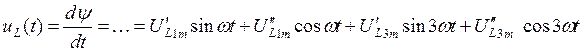Теперь составляется баланс коэффициентов для отдельных гамоник (уравнения гар­монического баланса) в соответствии со 2-м законом Кирхгофа u(t) = u_R(t) + u_L(t):

,

,

,

.

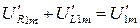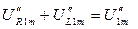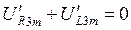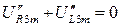В алгебраических уравнениях гармонического баланса отдельные слагае­мые в левой части являются некоторыми функциями неизвестных коэффициен­тов В₁, С₁, В₃, С₃. Решение этой системы уравнений представляет зачастую большую математическую трудность.

В виду больших математических осложнений, возникающих при опреде­лении неиз­вестных коэффициентов, метод гармонического баланса оказывается мало эффективным и применяется редко.