Дифференциального уравнения

Сущность данного метода заключается в том, что в нелинейном диффе­ренциальном уравнении, описывающем переходной процесс, пренебрегают не­линейностью второстепен­ных членов этого уравнения, при этом функциональ­ные коэффициенты в этих членах заме­няются постоянными. После такой за­мены нелинейное дифференциальное уравнение пре­вращается в линейное и ре­шается известными методами (классическим или операторным).

Рассмотрим применение данного метода на примере расчета переходного тока в трансформаторе при его включении на холостом ходу к источнику сину­соидального напря­жения 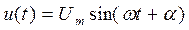(рис. 245а).

Дифференциальное уравнение цепи имеет вид: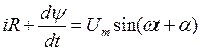

Так как активное сопротивление R обмотки трансформатора незначи­тельно, то 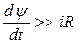и второе слагаемое iR можно считать второстепенным чле­ном этого уравнения.

Выразим 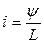, где L = f (i,y) – функциональный коэффициент, тогда дифференци­альное уравнение цепи получит вид:

.

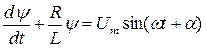Заменим функциональный коэффициент L = f(i,y) в последним уравнении некоторым постоянным значением L = L 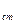= const, после чего дифференциаль­ное уравнение цепи стано­вится линейным относительно переменной ψ. Решение этого уравнения может быть получено классическим методом:

,

где , .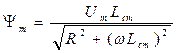

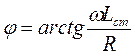В момент включения трансформатора y(0)=0 и, следовательно, постоян­ная интегриро­вания будет равна 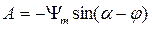. Таким образом амплитуда сво­бодной составляющей А зависит от начальной фазы напряжения источника. При a - j = 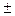90° она имеет максималь­ные значения, переходной процесс при этом протекает с максимальной интенсивностью. Пусть a - j = -90°, тогда А = Ψ_m и решение для функции y_(t) получит вид:

.

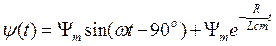Графическая диаграмма расчетной функции y(t) показана на рис. 248а.

Графическую диаграмму искомой функции i(t)можно построить методом проекции расчетной функции y(t)на вебер-амперную характеристику i(y)(рис. 248а, б). Эта диаграмма представлена на рис. 249:

Как показывает анализ полученного решения, амплитуда первой волны потокосцепле­ния практически равна удвоенному номинальному значению: 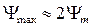. Эта точка 1 на ве­бер-амперной характеристике i(y) находится да­леко в области насыщения и ей соответствует ток I_max, значительно превышаю­щий амплитуду тока установившегося режима ( 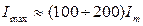), что при­мерно в 10 раз больше амплитуды номинального тока. Такой импульс пуско­вого тока совершенно не опасен для динамической или термической устойчи­вости транс­форматора, однако он может вызвать ложное срабатывание его ре­лейной за­щиты. По этой причине мощные силовые трансформаторы запреща­ется вклю­чать в сеть в режиме холостого хода. При включении в сеть нагру­женного трансформатора переходной процесс быстро затухает, при этом ампли­туда им­пульса пускового тока незначительна.