Расчет мгновенных значений параметров режима методом
численного интегрирования системы дифференциальных уравнений.
Режим нелинейной цепи любой сложности может быть описан системой нелинейных дифференциальных уравнений, составленных для схемы цепи по законам Кирхгофа. Как известно из математики, система дифференциальных уравнений (как линейных так и нелинейных) может быть решена методом численного интегрирования (методы Эйлера, Рунге-Кутта). Таким образом, режим любой нелинейной цепи может быть рассчитан методом численного интегрирования дифференциальных уравнений .
 Рассмотрим применение этого метода на примере расчета схемы рис. 244. Пусть на входе схемы источник синусоидальной ЭДС e(t) = Em·sin(wt), а вебер-амперная характеристика нелинейной катушки аппроксимирована уравнением i = a·sh(b·y).
Рассмотрим применение этого метода на примере расчета схемы рис. 244. Пусть на входе схемы источник синусоидальной ЭДС e(t) = Em·sin(wt), а вебер-амперная характеристика нелинейной катушки аппроксимирована уравнением i = a·sh(b·y).
Система дифференциальных уравнений, составленных для схемы цепи по законам Ома и Кирхгофа и дополненная нелинейным алгебраическим уравнением аппроксимации характеристики нелинейного элемента будет иметь вид:
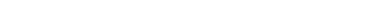
Решение этой системы уравнений может быть выполнено методами численного интегрирования на ЭВМ (например, методом Эйлера). Суть метода состоит в том, что период переменного тока Т разбивается на большое число шагов интегрирования, например N=1000, дифференциалы переменных заменяются конечными приращениями (dyÞDy, duÞDu, diÞDi, dtÞDt),апроизводные переменных - отношением приращений (dy/dtÞDy/Dt, du/dtÞDu/Dt). На каждом шаге производится решение системы уравнений и определяются значения переменных величин (токов, напряжений) и их производных, причем в качестве исходных данных принимают значения некоторых переменных на предыдущем шаге. В качестве таких функций принимают uС(t), iL(t),которые определяют запасы энергии в электрическом и магнитном поле, вследствие чего они не могут изменяться скачкообразно. Непосредственным результатом расчета будут являться массивы значений переменных величин (токов, напряжений) и их производных в заданном интервале времени (например, в течение периода Т). В результате последующей обработки массивов данных могут быть определены действующие, средние, максимальные значения переменных, их гармонический состав и другие параметры функций.
Метод численного интегрирования (численный метод) обладает высокой точностью, так как в нем непосредственно используются физические характеристики нелинейных элементов. С появлением ЭВМ и расширением области их применения данный метод является основным при расчете нелинейных цепей как в установившемся, так и в переходном режиме.
Один из вариантов решения полученной системы уравнений методом численного интегрирования представлен ниже.
Исходные данные: параметры элементов схемы (Em , f , R, C, a, b);начальные условия uС(0)=0, y(0)=0.
Принимаем: N-число шагов интегрирования за период тока, Т = 1/f - период тока, w=2pf- угловая частота,h=Dt=T/N- шаг интегрирования.
Алгоритм решения системы для произвольного к-го шага:
tк = h·к;
из (5) iк = a·sh(b·y(к-1));
из (2) uR к = iк ·R;
из (1) uLк = Em·sin(wtк)- uRк - uRок -uС(к-1);
из (3)(dy/dt) к = uLк;
из (4)(duС/dt) к = iк / C;
yк= y(к-1) + h · (dy/dt) к;
uСк = uС(к-1) + h · (duС/dt) к.
Вычисление определенных интегралов для определения действующих и средних значений переменных (здесь и далее на примере тока i):
Si1=Si1+ iк · iк ·h
Si2=Si2+ iк ·h
Вычисление определенных интегралов для определения гармонических спектров переменных:
для 1-й гармоники: Si3=Si3+ iк ·sin(1 ·wtк ) ·h
Si4=Si4+ iк ·cos(1·wtк ) ·h
для 2-й гармоники: Si5=Si5+ iк ·sin(2·wtк ) ·h
Si6=Si6+ iк ·cos(2·wtк ) ·h, и т.д.
Определение максимальных значений переменных:
если iк > Im то Im = iк.
Конец к-го цикла интегрирования.
После завершения процесса интегрирования производится вычисление интегральных параметров переменных.
Действующие значения: 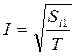 , и т. д.
, и т. д.
Cредние значения: 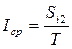 , и т. д.
, и т. д.
Амплитуды синусных и косинусных составляющих гармоник:
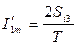 ;
; 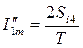 ;
; 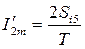 ;
; 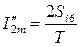 , и т.д.
, и т.д.
Амплитуды и начальные фазы гармоник:
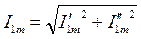 ;
; 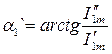 ;
; 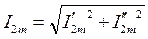 ;
; 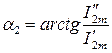 , и т.д.
, и т.д.
Действующие значения высших гармоник:
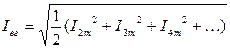 , и т.д.
, и т.д.
Коэффициенты амплитуды: Ка=Imax / I , и т.д.
Коэффициенты отдельных гармоник: Кг2 =I2m / I1m , Кг3 =I3m / I1m, и т.д.
Коэффициенты искажения: Ки = Iвг /I, и т.д.
Коэффициенты формы: Кф = I / Iср, и т.д.
Дата добавления: 2020-07-18; просмотров: 534;











