Расчет переходных процессов методом переменных состояния

Уравнениями состояния электрической цепи называют любую систему дифференци­альных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.

В более узком смысле в математике уравнениями состояния называют систему диф­ференциальных уравнений 1-го порядка, разрешенных относи­тельно производных (форма Коши). Система уравнений состояния в обобщен­ной форме имеет вид:

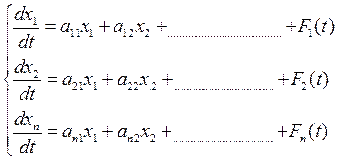
Та же система уравнений в матричной форме:

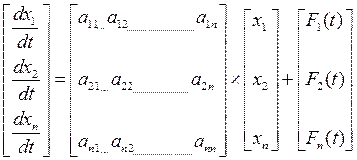
или в обобщённой матричной форме:

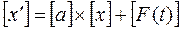
Система уравнений состояния формы Коши решается методом числен­ного интегри­ро­вания (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стан­дартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по сле­дующему алгоритму (метод Эйлера) для к-го шага:

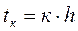
Значения производных на к-ом шаге:

…………………………………………………

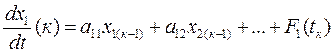
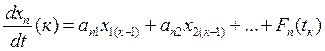
Значения переменных на к-ом шаге:

…………………………….

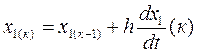
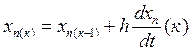
Для определения значений переменных и их производных на 1-м шаге ин­тегрирова­ния используются их значения на момент t=0, т.е. их начальные усло­вия .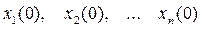

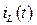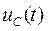Уравнения состояния формы Коши для заданной схемы могут быть полу­чены из сис­темы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются ''лишние'' переменные, имеющие зависимые начальные условия, и оставляют переменные и , которые не изменяются скачком и имеют независи­мые начальные условия 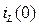, 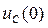; б) оставшиеся уравнения решаются от­но­сительно производных и приводятся их к форме Коши.

В случае сложных схем уравнения состояния формы Коши могут быть состав­лены топологическими методами с использованием матриц соеди­нени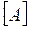й и .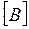

Последовательность расчета переходного процесса методом переменных состояния выглядит так:

1. Производится расчет схемы в установившемся режиме до коммута­ции и опре­деляются независимые начальные условия 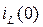и .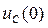

2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.

3. Методом исключения ''лишних'' переменных система уравнений Кирхгофа пре­образуется в систему уравнений Коши, составляются матрицы ко­эффициентов.

4. Выбирается расчетное время (продолжительность переходного про­цесса) и число шагов интегрирования N.

5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы 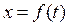или в виде таблицы координат функций для заданных моментов времени.

Пример. Для схемы рис. 154 с заданными параметрами элементов 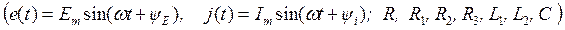выпол­нить расчет пере­ход­ного процесса и определить функцию .

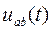1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия .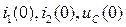

2. Составляется система дифференциальных уравнений по законам Кирхгофа:

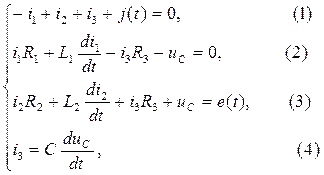
3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.

Для этой цели из (1) выражаем 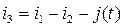и делаем подстановку в (2) и (3), а из (4) делаем подстановку в (1). Тогда получим:

из (2)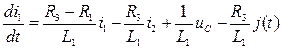

из (3)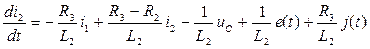

из (1)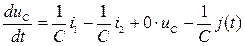

Введем обозначения: i₂=x₁; i₂=x₂; u_C=x₃. Подсчитаем значения отдель­ных коэффи­ци­ентов.

; ;

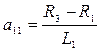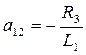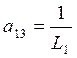
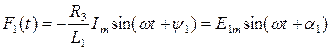, и т.д.

Составляем матрицы коэффициентов:

;

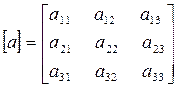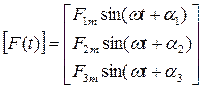
В качестве исследуемого промежутка времени выбираем период пере­менного тока 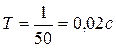. Число шагов интегрирования принимаем N=1000.

Вводим исходные данные в ЭВМ и выполняем расчет.

В качестве выходной функции принимаем:

.

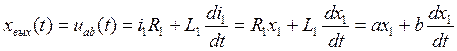Для выходной функции 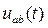строим графическую диаграмму в интер­вале периода Т.