Определение постоянных интегрирования
Определение постоянных интегрирования производится на заключительном этапе расчета переходного процесса, когда остальные составляющие решения уже найдены. Постоянные интегрирования определяются путем подстановки в решение для искомой функции соответствующих начальных условий.
Пусть решение для искомой функции i(t) содержит только одну постоянную интегрирования:
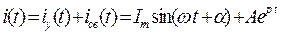
Постоянная интегрирования находится путем подстановки в решение начального условия для самой функции, т.е. i(0):
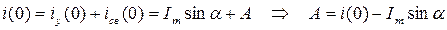 .
.
Пусть решение для искомой функции i(t) содержит две постоянных интегрирования и имеет вид:
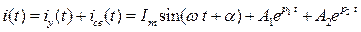
Постоянные интегрирования в этом случае находятся путем подстановки в решение начальных условий для самой функции i(0) и для ее первой производной 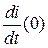 :
:

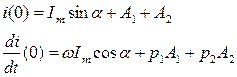
В результате совместного решения этой системы уравнений определяют искомые постоянные интегрирования А1 и А2 .
Последовательность выполнения отдельных этапов расчета переходных процессов классическим методом показана ниже в виде диаграммы.
Примечания:1. Выполнение всех этапов, обозначенных в диаграмме клетками, является обязательным и необходимым.
2. Выполнение первых пяти этапов, находящихся в верхнем горизонтальном ряду диаграммы, может производиться в любой последовательности, так как они не зависят друг от друга.
Пример. Для схемы рис. 132 с заданными параметрами элементов: Е=100 В, R=50 Ом, R1=20 Ом, R2=30 Ом, С=83,5 мкФ, определить ток i1 после коммутации.

1)Общий вид решения для искомой функции:
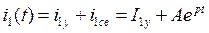
2)Определение установившейся составляющей из  расчета схемы после коммутации:
расчета схемы после коммутации:
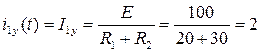 А
А
3)Характеристическое уравнение и его корень:
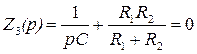 ,
, 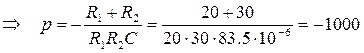 с-1
с-1
4)Независимое начальное условие uс(0) из расчета схемы до коммутации:
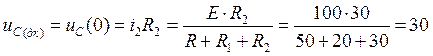 В
В
5)Система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации:

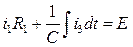 (1)
(1)
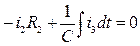 (2)
(2)
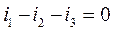 (3)
(3)
6)Начальное условие i1(0), необходимое для определения постоянной интегрирования из уравнения (1):
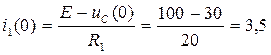 А
А
7)Определение постоянной интегрирования:
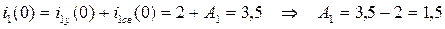 А
А
8)Решение для искомой функции:
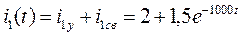
9)Графическая диаграмма искомой функции i1(t) показана на рис. 133:

9. Операторный метод расчета переходных процессов
Если система дифференциальных уравнений, которыми описывается переходной процесс в схеме, решается операционным методом, то и сам метод расчета переходного процесса также называется операционным или операторным.
Сущность операторного метода состоит в том, что на 1-ом этапе действительные функции времени i(t), u(t), называемые оригиналами, заменяются некоторыми новыми функциями I(p),U(p), называемыми операторными изображениями. Соответствие между оригиналом функции f(t) и ее операторным изображением F(p) устанавливается на основе прямого преобразования интеграла Лапласа:
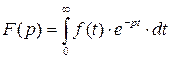 или
или 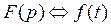 ,
,
где Û - знак соответствия; p=s+jw - комплексный оператор Лапласа.
Если s = 0, то p= jw, и преобразование Лапласа превращается в преобразование Фурье, которое лежит в основе комплексного метода расчета цепей переменного тока.
Преобразование Лапласа позволяет заменить операции 2-го рода над оригиналами функций (дифференцирование и интегрирование) на операции 1-го рода (умножение и деление) над операторными изображениями этих функций.
Расчет переходных процессов операторным методом условно выполняется в 3 этапа.
На 1-м этапе расчета система дифференциальных уравнений, составленная по законам Кирхгофа для оригиналов функций, после применения преобразования Лапласа превращается в систему алгебраических уравнений для операторных изображений этих функций.
На 2-ом этапе выполняется решение системы алгебраических операторных уравнений относительно искомой функции, в результате чего получают выражение искомой функции в операторной форме F(p).
На заключительном 3-м этапе выполняется обратный переход от найденного операторного решения для искомой функции F(p) к соответствующей ей функции времени f(t), т. е. Выполняется переход от изображения функции F(p)к ее оригиналу f(t).
Теоретически обратный переход от операторного изображения функции F(p)к ее оригиналу f(t) устанавливается на основе обратного преобразования Лапласа:
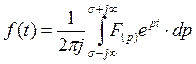 .
.
На практике для обратного перехода используются более простые и удобные методы, а именно: формула разложения и таблицы соответствия.
Дата добавления: 2020-07-18; просмотров: 898;











