Переходные функции по току и напряжению
Пусть произвольная электрическая цепь с нулевыми начальными условиями 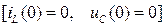 в момент времени
в момент времени 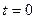 включается под действием источника постоянной ЭДС
включается под действием источника постоянной ЭДС 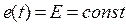 (рис. 148).
(рис. 148).

Переходной процесс не изменится, если из схемы убрать ключ, а постоянную ЭДС 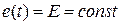 заменить скачкообразной
заменить скачкообразной 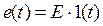 со скачком в момент
со скачком в момент 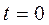 (рис. 149).
(рис. 149).

 Функция
Функция 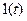 называется единичной скачкообразной функцией, имеющей значения:
называется единичной скачкообразной функцией, имеющей значения:
Возникающие на любых участках цепи токи 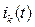 и напряжения
и напряжения 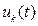 прямо пропорциональны скачкообразной ЭДС
прямо пропорциональны скачкообразной ЭДС 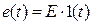 :
:
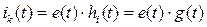
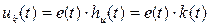
где 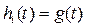 - переходная функция по току, или переходная проводимость,
- переходная функция по току, или переходная проводимость, 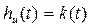 - переходная функция по напряжению.
- переходная функция по напряжению.
Переходная функция по току 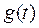 или по напряжению
или по напряжению 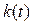 называется функция по времени, численно равная соответствующему току
называется функция по времени, численно равная соответствующему току 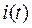 или напряжению
или напряжению 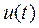 при включении цепи с нулевыми начальными условиями к источнику единичной постоянной
при включении цепи с нулевыми начальными условиями к источнику единичной постоянной 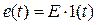 . Переходные функции
. Переходные функции 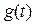 и
и 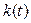 могут быть рассчитаны для любой схемы классическим или операторным методом.
могут быть рассчитаны для любой схемы классическим или операторным методом.
Пример.Рассчитать переходные функции для тока 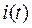 и напряжения
и напряжения 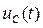 в цепи R,С.
в цепи R,С.
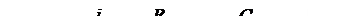
Выполним расчет переходного процесса в цепи R, C при включении ее к источнику постоянной ЭДС 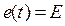 (рис. 3) классическим методом. В результате найдем:
(рис. 3) классическим методом. В результате найдем:
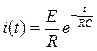 ;
; 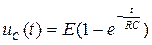 .
.
Искомые переходные функции получим из найденных выражений, заменив в них Е на 1.
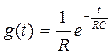 ;
; 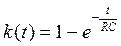 .
.
Переходные функции используются при расчете переходных процессов методом интеграла Дюамеля.
20. Расчет переходных процессов методом интеграла Дюамеля
Метод интеграла Дюамеля применяется для расчета переходных процессов в электрических цепях в том случае, если в рассматриваемой цепи действует источник ЭДС 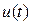 произвольной формы, отличной от стандартной (постоянной или синусоидальной).
произвольной формы, отличной от стандартной (постоянной или синусоидальной).
Пусть к источнику ЭДС произвольной формы 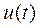 подключается цепь с нулевыми начальными условиями и с заданной переходной проводимостью
подключается цепь с нулевыми начальными условиями и с заданной переходной проводимостью 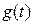 (рис. 4).
(рис. 4).
 Заменим непрерывную кривую ЭДС
Заменим непрерывную кривую ЭДС 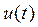 приближенно ступенчатой с интервалами по оси
приближенно ступенчатой с интервалами по оси 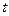 между отдельными скачками, равными
между отдельными скачками, равными 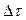 . Первый скачок ЭДС равен
. Первый скачок ЭДС равен 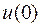 и действует в момент
и действует в момент 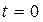 . Все последующие скачки ЭДС можно определить как
. Все последующие скачки ЭДС можно определить как 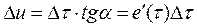 и действуют они с запаздыванием на
и действуют они с запаздыванием на 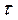 , то есть в момент
, то есть в момент 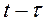 . Ток на выходе цепи в произвольный момент времени t можно рассматривать в соответствии с принципом наложения как сумму частичных токов, возникающих под действием отдельных скачков ЭДС, следующих друг за другом через промежутки
. Ток на выходе цепи в произвольный момент времени t можно рассматривать в соответствии с принципом наложения как сумму частичных токов, возникающих под действием отдельных скачков ЭДС, следующих друг за другом через промежутки 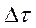 в интервале времени от 0 до t.
в интервале времени от 0 до t.
Частичный ток, вызванный первым источником ЭДС, будет равен 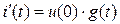 , а частичные токи, вызванные последующими скачками ЭДС, будут равны:
, а частичные токи, вызванные последующими скачками ЭДС, будут равны: 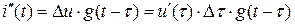 .
.
Результирующий ток равен сумме частичных токов:
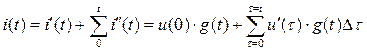 .
.
Перейдем к бесконечно малым интервалам 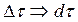 и заменим сумму интегралом:
и заменим сумму интегралом:
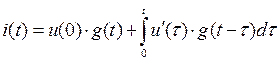 .
.
Полученное выражение для 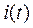 носит название интеграла Дюамеля и применяется на практике для расчета переходных процессов в электрических цепях при воздействии на них источников ЭДС или тока произвольной формы.
носит название интеграла Дюамеля и применяется на практике для расчета переходных процессов в электрических цепях при воздействии на них источников ЭДС или тока произвольной формы.
Порядок применения интеграла Дюамеля:
1) Выполняют расчет переходного процесса классическим или операторным методом при включении исследуемой цепи к источнику единичной постоянной ЭДС 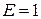 и таким образом определяют необходимую переходную функцию по току
и таким образом определяют необходимую переходную функцию по току 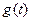 или по напряжению
или по напряжению 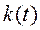 .
.
2) Определяют переходную функцию 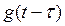 или
или 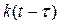 путем замены в выражениях
путем замены в выражениях 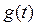 или
или 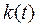 переменной
переменной 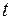 на
на 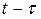 .
.
3) Находят производную от функции ЭДС 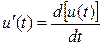 и в полученном выражении заменяют переменную t на t, в результате получают функцию
и в полученном выражении заменяют переменную t на t, в результате получают функцию 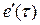 .
.
4) Выражения функций 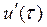 ,
, 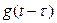 или
или 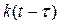 подставляют в формулу интеграла Дюамеля, выполняют интегрирование по переменной
подставляют в формулу интеграла Дюамеля, выполняют интегрирование по переменной 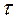 и подставляют пределы интегрирования по переменной t. При необходимости упрощают структуру полученного выражения искомой функции
и подставляют пределы интегрирования по переменной t. При необходимости упрощают структуру полученного выражения искомой функции 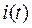 или
или 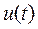 .
.
Замечания:
1) Если функция 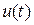 претерпевает скачки или разрывы, то она разбивается на отдельные участки с плавным изменением функции, при этом интеграл Дюамеля применяется к каждому участку в отдельности.
претерпевает скачки или разрывы, то она разбивается на отдельные участки с плавным изменением функции, при этом интеграл Дюамеля применяется к каждому участку в отдельности.
2) При расчете переходных процессов в цепях постоянного или синусоидального тока метод интеграла Дюамеля проигрывает классическому и операторному методам, поэтому для таких цепей он не применяется.
Пример. Рассчитать ток 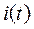 в цепи R, C при действии на нее трапециевидного импульса с заданными параметрами (рис. 152):
в цепи R, C при действии на нее трапециевидного импульса с заданными параметрами (рис. 152):

Переходная проводимость схемы:
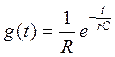 ;
; 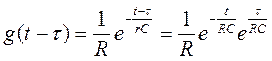 .
.
Производная от функции ЭДС 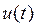 :
: 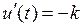 ;
; 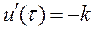 .
.
Так как функция 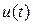 в момент времени
в момент времени 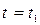 изменяется скачком, то ее разбиваем на два участка
изменяется скачком, то ее разбиваем на два участка 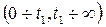 , для каждого из которых находим свое решение для искомой функции
, для каждого из которых находим свое решение для искомой функции 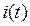 .
.
Решение для 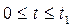 :
:
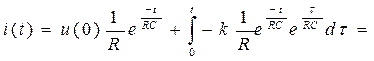
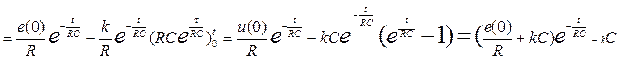
Решение для 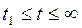 :
:
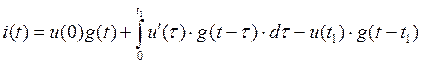
Дата добавления: 2020-07-18; просмотров: 697;











