Расчет переходных процессов методом численного интегрирования

дифференциаль­ных уравнений на ЭВМ

Система дифференциальных уравнений, которыми описывается состоя­ние лю­бой электрической цепи, может быть решена методом численного интег­рирования на ЭВМ (ме­тод последовательных интервалов или метод Эйлера).

Сущность метода состоит в том, что исследуемый промежуток времени Т (при расчете переходных процессов, это Т_п - продолжительность переходного процесса) разбива­ется на большое число N элементарных отрезков времени 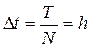, которые называются шагом интегрирования.

В дифференциальных уравнениях дифференциалы функций заменяются их конеч­ными приращениями, а производные функций - отношениями прира­щений:

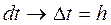
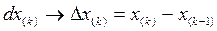
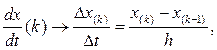откуда следует:

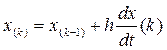
На каждом шаге интегрирования решается система дифференциальных уравнений, в результате решения определяются численные значения производ­ных и самих функций. В качестве исходных данных для их определения ис­пользуются значения этих же функций на предыдущем шаге, а на начальном 1-ом шаге – их значения в момент коммута­ции при t =0 , т.е. начальные условия. В результате расчета для функций и их производных составляются массивы их значений в исследуемом интервале времени Т, которые после за­вершения цикла подвергаются соответствующей математической обработке, а именно: стро­ятся графические диаграммы функций, составляются необходимые таблицы, иссле­дуются функции на наличие максимумов и минимумов, устанавливается про­должительность пере­ходного процесса и его характер, и т.д.

Пример. Рассчитать переходный процесс в схеме рис. 153 с заданными па­раметрами элементов: 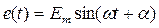, R₁, R₂, R₃, L₁, L₂, С.

Путем расчета схемы в установившемся режиме до коммутации опреде­ляются неза­висимые начальные условия .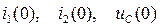

По законам Кирхгофа для схемы после коммутации составляется система дифферен­циальных уравнений:

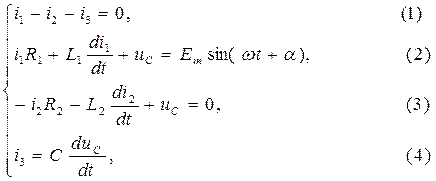
Выбирается шаг интегрирования h (например, из расчета N=1000 шагов на период Т=0,02 с переменного тока, тогда h=Т/ N =2·10^-5 с).

Составляется алгоритм вычислений для произвольного к-го шага:

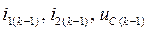- исходные данные,

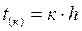- текущее время,

,

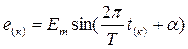из (1) ,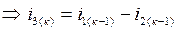

из (2) ,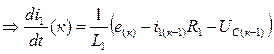

из (3) ,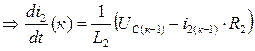

из (4) ,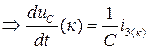

,

,

.

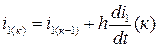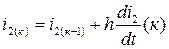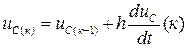Далее следуют вычисления по тому же алгоритму для (к+1)-го шага и т. д.

В соответствии с составленным алгоритмом на любом языке составляется программа вычислений на ЭВМ, что представляет собой несложную инженер­ную задачу.

В настоящее время метод численного интегрирования является наиболее уни­версаль­ным и наиболее простым методом расчета переходных процессов в электрических цепях. Достоинствами метода являются:

1. Метод численного интегрирования одинаково просто может приме­няться для расчета переходных процессов в электрических цепях любой слож­ности, содержащих любое число независимых накопителей энергии L и C. В то же время в классическом и операторном методах с увеличением числа незави­симых накопителей энергии (и соответст­венно порядка дифференциального уравнения) значительно возрастают математические сложности, что практиче­ски не позволяет применять эти методы для решения дифференци­альных урав­нений выше 2-го порядка.

2. Метод численного интегрирования позволяет сравнительно просто выполнить математический анализ решения для искомой функции и получить выводы, необходимые для инженерной практики, а именно: определить харак­тер и продолжительность переходного процесса, определить максимальные зна­чения функции и т.д.

К недостаткам метода следует отнести необходимость составления ин­дивидуальной расчетной программы для каждой конкретной задачи и решение ее на ЭВМ, что сегодня уже посильно каждому инженеру.