Алгоритм расчета переходных процессов операторным методом

Замечания к формуле разложения.
1) Если в исходной схеме имеются источники постоянных ЭДС Е, то уравнение 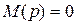 может иметь один корень, равный нулю (
может иметь один корень, равный нулю ( 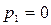 ). Подстановка этого корня в формулу разложения дает постоянную величину
). Подстановка этого корня в формулу разложения дает постоянную величину 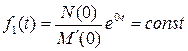 , которая соответствует установившейся составляющей искомой функции.
, которая соответствует установившейся составляющей искомой функции.
2) Если в исходной схеме имеются источники синусоидальных ЭДС 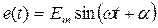 , то уравнение
, то уравнение 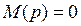 будет иметь два чисто мнимых и сопряженных корня
будет иметь два чисто мнимых и сопряженных корня 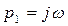 и
и 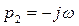 . Подстановка этих корней в формулу разложения в сумме дает синусоидальную функцию времени, которая соответствует установившейся составляющей искомой функции:
. Подстановка этих корней в формулу разложения в сумме дает синусоидальную функцию времени, которая соответствует установившейся составляющей искомой функции:
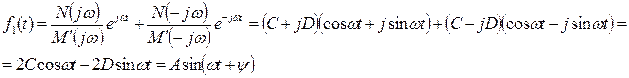
3) Если уравнение 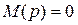 имеет два комплексно сопряженных корня
имеет два комплексно сопряженных корня 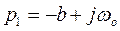 и
и 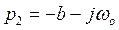 , то подстановка этих корней в формулу разложения в сумме дает синусоидальную функцию с затухающей амплитудой:
, то подстановка этих корней в формулу разложения в сумме дает синусоидальную функцию с затухающей амплитудой:
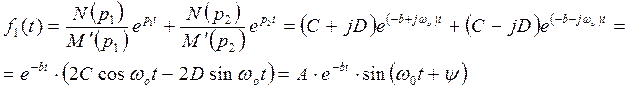
4) Если уравнение 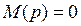 имеет кратные корни (
имеет кратные корни ( 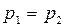 ), то формула разложения неприменима. Случай кратных корней может встретиться в практике крайне редко. Чтобы применить формулу разложения в этом случае достаточно несущественно изменить параметры одного из элементов схемы.
), то формула разложения неприменима. Случай кратных корней может встретиться в практике крайне редко. Чтобы применить формулу разложения в этом случае достаточно несущественно изменить параметры одного из элементов схемы.
Пример.Для схемы рис. 138 с заданными параметрами элементов (Е=100 В, R=50 Ом, R1=20 Ом, R2=30 Ом, С=83,5 мкФ) определить ток 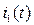 после коммутации.
после коммутации.

1) Определяется независимое начальное условие 
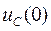 из расчета схемы рис. 138 в состоянии до коммутации:
из расчета схемы рис. 138 в состоянии до коммутации:
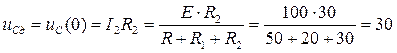 B
B
2) Составляется операторная схема цепи после коммутации (рис. 139):
3) Составляется система контурных уравнений для схемы рис. 139 в операторной форме:

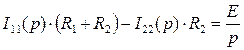
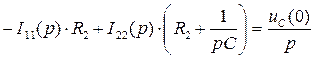
4) Производится решение операторных уравнений относительно искомой функции I1(p):
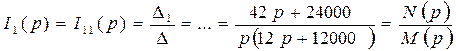 ,
,
где 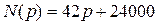 ;
; 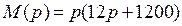 ;
; 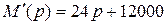
5) Корни уравнения 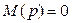 :
:
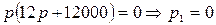 ;
; 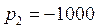
6) Коэффициенты 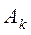 для отдельных корней pk:
для отдельных корней pk:
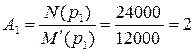 ;
; 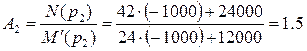
7) Окончательное решение для искомой функции времени:
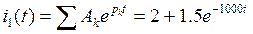 A
A
15. Анализ переходных процессов в цепи R, L
Исследуем, как изменяется ток 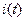 в цепи с резистором R и катушкой L в переходном режиме. В качестве примера рассмотрим переходной процесс при включении цепи R, L к источнику а) постоянной ЭДС
в цепи с резистором R и катушкой L в переходном режиме. В качестве примера рассмотрим переходной процесс при включении цепи R, L к источнику а) постоянной ЭДС 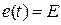 =const и б) переменной ЭДС
=const и б) переменной ЭДС 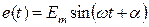 (рис. 140).
(рис. 140).
Расчет переходного процесса выполним классическим методом.
а) Включение цепи R, L к источнику постоянной ЭДС 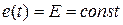 .
.
Общий вид решения для тока: 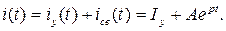
Установившаяся составляющая тока: 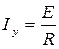 .
.
Характеристическое уравнение и его корни:
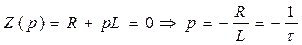 .
.
Независимое начальное условие: 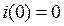 .
.
Постоянная интегрирования: 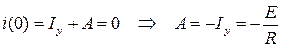 .
.
Окончательное решение для искомой функции:
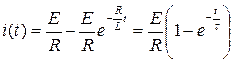 ,
,
где 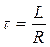 − постоянная времени, численно равная времени, за которое амплитуда свободной составляющей затухает в
− постоянная времени, численно равная времени, за которое амплитуда свободной составляющей затухает в 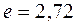 раза. Чем больше
раза. Чем больше 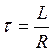 , тем медленнее затухает переходной процесс. Теоретически затухание свободной составляющей продолжается до бесконечности. Техническое время переходного процесса
, тем медленнее затухает переходной процесс. Теоретически затухание свободной составляющей продолжается до бесконечности. Техническое время переходного процесса 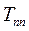 определяется из условия, что за это время свободная составляющая уменьшается до 0,01 от ее первоначального значения:
определяется из условия, что за это время свободная составляющая уменьшается до 0,01 от ее первоначального значения:
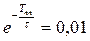 , откуда
, откуда 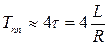 .
.
На рис. 141 представлена графическая диаграмма искомой функции 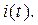

Для приближенного построения графической диаграммы свободной составляющей 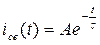 можно воспользоваться таблицей значений этой функции в интервале времени
можно воспользоваться таблицей значений этой функции в интервале времени 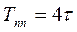 :
:
| t | 0,5 | 1,0 | 1,5 | ||||
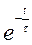
| 0,61 | 0,37 | 0,22 | 0,14 | 0,05 | 0,02 |
Постоянная времени 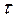 может быть определена из графической диаграммы функции
может быть определена из графической диаграммы функции 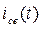 как отрезок времени
как отрезок времени 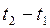 , по краям которого отношение значений функции равно
, по краям которого отношение значений функции равно 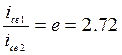 раза (рис. 141).
раза (рис. 141).
б) Включение цепи R, L к источнику синусоидальной ЭДС 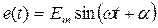
Общий вид решения для тока:
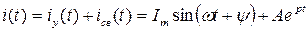
Характеристическое уравнение и его корни:
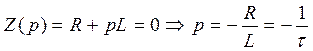
Установившаяся составляющая тока:
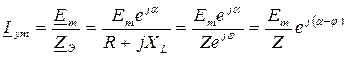 , откуда следует
, откуда следует
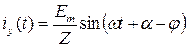 ,
,
где 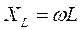 ,
, 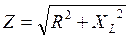 ,
, 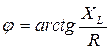 .
.
Независимое начальное условие: 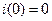
Постоянная интегрирования:
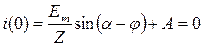 , откуда
, откуда 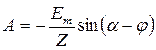
Окончательное решение для искомой функции:
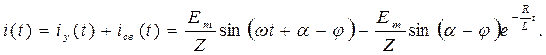
Из анализа решения видно, что амплитуда свободной составляющей А зависит от начальной фазы 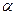 источника ЭДС. При
источника ЭДС. При 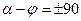 эта амплитуда имеет максимальное значение
эта амплитуда имеет максимальное значение 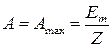 , при этом переходной процесс протекает с максимальной интенсивностью. При
, при этом переходной процесс протекает с максимальной интенсивностью. При 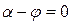 амплитуда свободной составляющей равна нулю, и переходной процесс в цепи вообще отсутствует. На рис. 142 представлена графическая диаграмма искомой функции
амплитуда свободной составляющей равна нулю, и переходной процесс в цепи вообще отсутствует. На рис. 142 представлена графическая диаграмма искомой функции 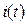 при
при 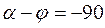 ,
, 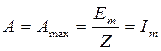 .
.

16. Анализ переходных процессов в цепи R, C
Исследуем характер переходных процессов в цепи R, C при включении ее к источнику а)постоянной ЭДС 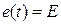 , б)переменной ЭДС
, б)переменной ЭДС 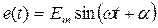 (рис. 143).
(рис. 143).
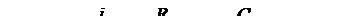
а) Включение цепи R, C к источнику постоянной ЭДС 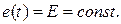
Общий вид решения для напряжения 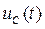 :
:
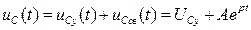 .
.
Установившаяся составляющая напряжения: 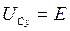 :
:
Характеристическое уравнение и его корни:
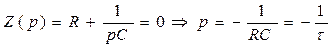 , где
, где 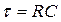 - постоянная времени.
- постоянная времени.
Независимое начальное условие: 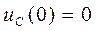 .
.
Постоянная интегрирования: 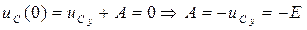 .
.
Окончательное решение для искомой функции:
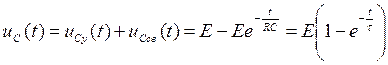 ,
,
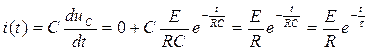 .
.
Подсчитаем баланс энергий при зарядке конденсатора.
Энергия источника ЭДС:
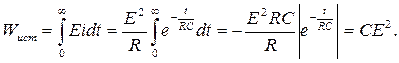
Энергия, выделяемая в резисторе R в виде тепла:
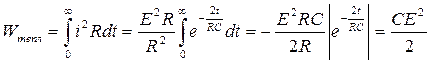 .
.
Энергия электрического поля конденсатора:
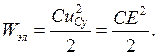
Таким образом, энергия электрического поля конденсатора составляет ровно половину энергии источника 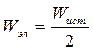 и не зависит от величины сопротивления зарядного резистора R (закон половины).
и не зависит от величины сопротивления зарядного резистора R (закон половины).
Графические диаграммы функций 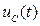 и
и 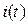 показаны на рис. 144.
показаны на рис. 144.
б) Включение цепи R, C к источнику синусоидальной ЭДС 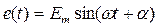 .
.
Общий вид решения для напряжения 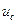 :
:
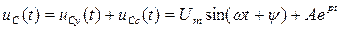

Характеристическое уравнение и его корень:
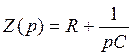
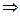
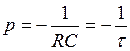
Установившаяся составляющая напряжения:
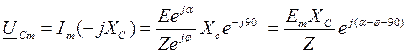 , откуда
, откуда
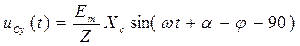 ,
,
где 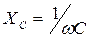 ,
, 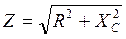 ,
, 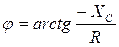 .
.
Независимое начальное условие: 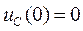 .
.
Определение постоянной интегрирования:
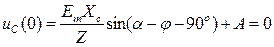 ; откуда
; откуда 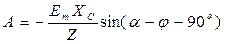 .
.
Как следует из полученного уравнения, амплитуда свободной составляющей 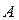 зависит от начальной фазы
зависит от начальной фазы 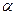 источника ЭДС. При
источника ЭДС. При 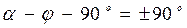 эта амплитуда имеет максимальное значение
эта амплитуда имеет максимальное значение 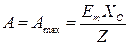 , при этом переходной процесс протекает с максимальной интенсивностью. При
, при этом переходной процесс протекает с максимальной интенсивностью. При 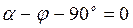 амплитуда свободной составляющей равна нулю и переходной процесс в цепи отсутствует.
амплитуда свободной составляющей равна нулю и переходной процесс в цепи отсутствует.
18. Анализ переходных процессов в цепи R, L, C
Переходные процессы в цепи R, L, C описываются дифференциальным уравнением 2-го порядка. Установившиеся составляющие токов и напряжений определяются видом источника энергии и определяются известными методами расчета установившихся режимов. Наибольший теоретический интерес представляют свободные составляющие, так как характер свободного процесса оказывается существенно различным в зависимости от того, являются ли корни характеристического уравнения вещественными или комплексными сопряженными.
Проанализируем переходной процесс в цепи R, L, C при включении ее к источнику постоянной ЭДС (рис. 145).

Общий вид решения для тока: 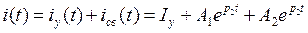 .
.
Установившаяся составляющая: 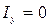 .
.
Характеристическое уравнение и его корни: 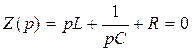 , откуда:
, откуда:
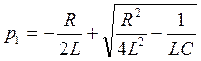 ;
; 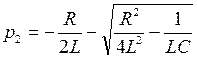 .
.
Дифференциальное уравнение: 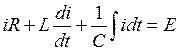 .
.
Независимые начальные условия: 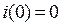 ;
; 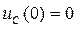 .
.
Зависимое начальное условие: 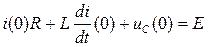 ; откуда
; откуда 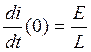 .
.
Постоянные интегрирования определяется из соместного решения системы уравнений:


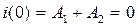
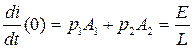 , откуда
, откуда 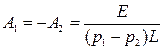 .
.
Окончательное решение для тока:
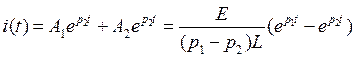 .
.
Исследуем вид функции 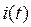 при различных значениях корней характеристического уравнения.
при различных значениях корней характеристического уравнения.
а) Корни характеристического уравнения вещественные, не равны друг другу. Это имеет место при условии 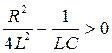 или
или 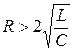 , тогда
, тогда 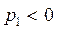 ,
, 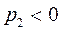 , причем
, причем 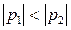 ,
, 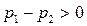 .
.
При изменении t от 0 до ∞ отдельные функции 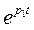 и
и 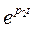 убывают по экспоненциальному закону от 1 до 0, причем вторая из них убывает быстрее, при этом их разность
убывают по экспоненциальному закону от 1 до 0, причем вторая из них убывает быстрее, при этом их разность 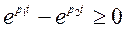 . Из этого следует вывод, что искомая функция тока
. Из этого следует вывод, что искомая функция тока 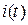 в крайних точках при t = 0 и при t = ∞ равна нулю, а в промежутке времени 0 < t < ∞ - всегда положительна, достигая при некотором значении времени
в крайних точках при t = 0 и при t = ∞ равна нулю, а в промежутке времени 0 < t < ∞ - всегда положительна, достигая при некотором значении времени 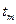 своего максимального значения
своего максимального значения 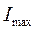 . Найдем этот момент времени:
. Найдем этот момент времени:
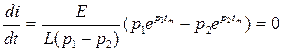 , или
, или 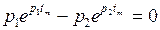 , откуда
, откуда 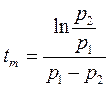 .
.
Графическая диаграмма функции 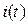 для случая вещественных корней характеристического уравнения показана на рис. 146.
для случая вещественных корней характеристического уравнения показана на рис. 146.

Продолжительность переходного процесса в этом случае определяется меньшим по модулю корнем: 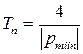 .
.
Характер переходного процесса при вещественных корнях характеристического уравнения получил название затухающего или апериодического.
б) Корни характеристического уравнения комплексно сопряженные. Это имеет место при соотношении параметров 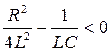 или
или 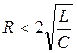 , тогда
, тогда
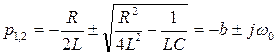 ,
,
где 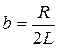 - коэффициент затухания,
- коэффициент затухания, 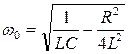 - угловая частота собственных колебаний.
- угловая частота собственных колебаний.
Решение для исконной функции может быть преобразовано к другому виду:
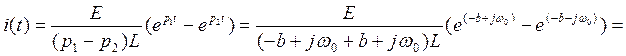
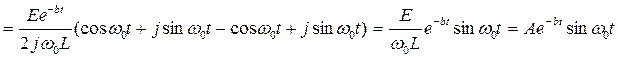 .
.
Таким образом, в случае комплексно сопряженных корней характеристического уравнения искомая функция 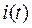 изменяется во времени по гармоническому закону
изменяется во времени по гармоническому закону 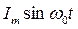 с затухающей амплитудой
с затухающей амплитудой 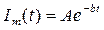 . Графическая диаграмма функции
. Графическая диаграмма функции 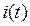 показана на рис. 147.
показана на рис. 147.

Период колебаний 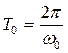 , продолжительность переходного процесса определяется коэффициентом затухания:
, продолжительность переходного процесса определяется коэффициентом затухания: 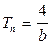 .
.
Характер переходного процесса при комплексно сопряженных корнях характеристического уравнения получил название колебательного или периодического.
В случае комплексно сопряженных корней для определения свободной составляющей применяют частную форму:
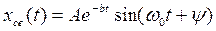 или
или 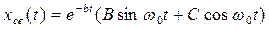 ,
,
где коэффициенты 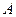 и
и 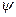 или
или 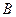 и
и 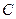 являются новыми постоянными интегрирования, которые определяются через начальные условия для искомой функции.
являются новыми постоянными интегрирования, которые определяются через начальные условия для искомой функции.
в) Корни характеристического уравнения вещественные и равны друг другу. Это имеет место при условии 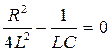 или
или 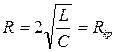 , тогда
, тогда 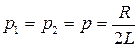 .
.
Полученное ранее решение для искомой функции 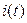 в этом случае становится неопределенным, так как числитель и знаменатель дроби превращаются в нуль. Раскроем эту неопределенность по правилу Лопиталя, считая
в этом случае становится неопределенным, так как числитель и знаменатель дроби превращаются в нуль. Раскроем эту неопределенность по правилу Лопиталя, считая 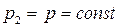 , а
, а 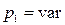 , которая стремится к
, которая стремится к 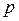 . Тогда получим:
. Тогда получим:
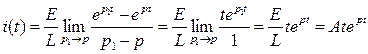 .
.
Характер переходного процесса при равных корнях характеристического уравнения получил название критического. Критический характер переходного процесса является граничным между затухающим и колебательным и по форме ничем не отличается от затухающего. Продолжительность переходного процесса 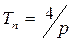 . При изменении только сопротивления резистора
. При изменении только сопротивления резистора 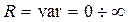 затухающий характер переходного процесса соответствует области значений
затухающий характер переходного процесса соответствует области значений 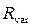
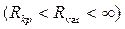 , колебательный характер - также области значений
, колебательный характер - также области значений 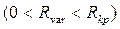 , а критический характер – одной точке
, а критический характер – одной точке 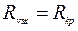 . Поэтому на практике случай равных корней характеристического уравнения встречается крайне редко.
. Поэтому на практике случай равных корней характеристического уравнения встречается крайне редко.
В случае равных корней для определения свободной составляющей применяют частную форму:
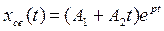 ,
,
где коэффициенты 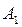 и
и 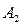 являются новыми постоянными интегрирования, которые определяются через начальные условия для искомой функции.
являются новыми постоянными интегрирования, которые определяются через начальные условия для искомой функции.
Критический режим переходного процесса характерен тем, что его продолжительность имеет минимальное значение 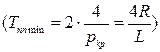 . Указанное свойство находит применение в электротехнике.
. Указанное свойство находит применение в электротехнике.
Дата добавления: 2020-07-18; просмотров: 950;











