Интерполяционный многочлен Ньютона

Интерполяционный многочлен Ньютона для равноотстоящих узлов в общем виде выглядит следующим образом:

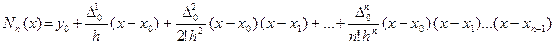, (3.3.1)

Пусть в соответствии с вариантом задания исходная функция задана в виде значений в диапазоне ячеек B7:C10, рис. 3.3.1.

Примечание: так как рассматривается формула Ньютона для равноотстоящих узлов, значения исходной таблицы соответствующим образом изменены.

Тогда выражение 3.3.1 примет вид

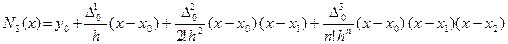, (3.3.2)

В ячейках M19,O19 и Q19вычислим конечные разности D¹₀, D²₀ и D³₀ для интерполяционного многочлена Ньютона N₃(x) для равноотстоящих узлов по формуле 3.2.2, как показано на рис. 3.3.1.

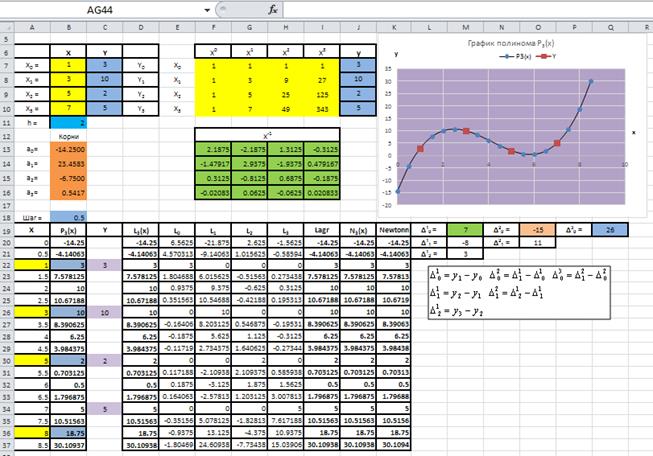
Рис. 3.3.1

В ячейку J20 запишем арифметическое выражение интерполяционного многочлена Ньютона N₃(x) для равноотстоящих узлов по формуле 3.2.2, при этом значения аргументов x₀, x₁,x₂ и y₀ взяты из ячеек диапазона B7:B9 и ячейки C7, в абсолютной адресации, а значение аргумента x взято из ячейки A20 в относительной адресации

=$C$7+$M$19/$B$11*(A20-$B$7)+$O$19/(2*$B$11^2)*(A20-$B$7)*(A20-$B$8)+$Q$19/(6*$B$11^3)*(A20-$B$7)*(A20-$B$8)*(A20-$B$9),

кроме того значение величины h, которая является шагом в исходной таблице равноотстоящих значений x₀, x₁,x₂ и x₃ вычисляется, например, в ячейке B11, как =B8-B7 и берётся в абсолютной адресации.

Полученное в ячейке J20 значение -14.25(исходная таблица изменена) и есть результат вычисления интерполяционного полинома Ньютона N₃(x) для равноотстоящих узлов для аргумента x = 0.

Скопируем закон преобразования информации ячейки J20 до J37 включительно.

Появившиеся в диапазоне ячеек J20:J37 значения, и есть значения интерполяционного полинома Ньютона N₃(x) для равноотстоящих узлов, вычисленные на спектре значений аргумента x диапазона ячеек A20:A37, (x Î[0;8.5]), рис. 3.3.1.

Полное совпадение значений диапазонов ячеек B20:B37 (канонический полином P₃(x)), D20:D37 (интерполяционный полином Лагранжа L₃(x) в среде Excel), I20:I37 (интерполяционный полином Лагранжа L₃(x) в средеVBA) и J20:J37 (интерполяционный полином Ньютона N₃(x) для равноотстоящих узлов в среде Excel) является доказательством правильности полученного решения варианта задания.

Совпадение значений ячеек B39, D39,I39 и J39 подтверждает правильность вычислений значений полиномов P₃(x), L₃(x), N₃(x) = 10.64, при x = 2.372, рис. 3.3.1.

Для вычисления значений интерполяционного полинома Ньютона N₃(x) для равноотстоящих узлов в среде VBA необходимо предварительно создать модуль VBA