Нахождение коэффициентов полинома решением СЛАУ

Пусть в соответствии с вариантом задания исходная функция задана в виде значений в диапазоне ячеек B7:C10, рис. 3.1.1.

Составим систему n + 1 уравнений с n + 1 неизвестными, для чего:

– в ячейку F7 запишем условие =ЕСЛИ(B7<0;1;B7^0), в данном случае это можно было и не делать, так по предложенному варианту задания ситуации 0⁰ не возникает;

– в ячейку G7 запишем арифметическое выражение =B7^1;

– в ячейку H7 запишем арифметическое выражение =B7^2;

– в ячейку I7 запишем арифметическое выражение =B7^3;

– выделим диапазон ячеек F7:I7 и скопируем законы преобразования информации ячеек диапазона до 10 строки включительно;

В результате получим матрицу значений аргументов x в степенях от 0до n, то есть до 3, рис. 3.1.1.

Значения функции y = f(x) просто скопируем из исходной таблицы, то есть

J7=C7, J8=C8, J9=C9, J10=C10.

Коэффициенты системы линейных алгебраических уравнений определены и, чтобы найти корни этой системы необходимо:

– с помощью мастера функций f_x в диапазоне ячеек F13:I16 сформировать матрицу обратную матрице аргументов x =МОБР(F7:I10);

– с помощью мастера функций f_x в диапазоне ячеек B13:B16 вычислить корни системы линейных алгебраических уравнений используя функцию =МУМНОЖ(F13:I16;J7:J10);

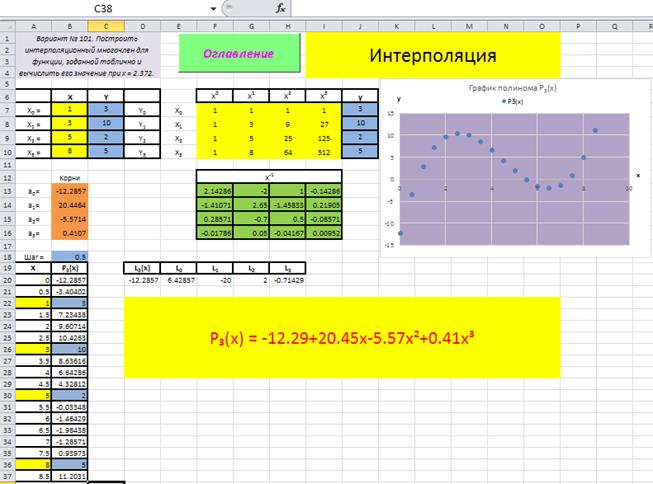
Рис. 3.1.1

Таким образом, корни системы линейных алгебраических уравнений, являющиеся коэффициентами интерполяционного полинома P₃(x), определены и их значения a₀ = -12.2857, a₁ = 20.4454,a₂ = -5.5714,a₃ = 0.4107 показаны в диапазоне ячеек B13:B16.

Чтобы “увидеть” аналитическое выражение полученного интерполяционного полинома P₃(x) объединим, например, ячейки диапазона D22:O28, и в объединённую ячейку запишем сцепленные символьные константы

="P₃(x) = "&ТЕКСТ($B$13;"0,00")& ЕСЛИ($B$14<0;ТЕКСТ($B$14;"0,00"); "+"&ТЕКСТ($B$14;"0,00"))&"x"&ЕСЛИ($B$15<0;ТЕКСТ($B$15;"0,00");"+"&ТЕКСТ($B$15;"0,00"))&"x²"&ЕСЛИ($B$16<0;ТЕКСТ($B$16;"0,00");"+"&ТЕКСТ($B$16;"0,00"))&"x³"

В результате в объединённой ячейке получим

P₃(x) = -12.29 + 20.45 x – 5.57 x² + 0.41 x³

Чтобы проверить правильность решения, вычислим спектр значений полученного интерполяционного полинома P₃(x)на спектре значений аргумента x Î[0;8.5]. Начальное значение диапазона 0 и конечное 8.5 выбираются такими, чтобы “накрыть” диапазон исходной таблицы x Î[x₀;x₃]. Шаг табулирования, в данном случае 0.5, выбирается таким, чтобы “попасть” в узлы интерполяции.

Тогда, оформив в ячейках A19 и B19 шапку таблицы, как показано на рис. 3.1.1, ячейках A20 и A37 получим спектр значений аргумента x.

В ячейку B20 запишем арифметическое выражение интерполяционного полинома P₃(x) =$B$13+$B$14*A20^1+$B$15*A20^2+$B$16*A20^3 с коэффициентами, взятыми в абсолютной адресации из ячеек B13:B16 и аргументом x, взятым в относительной адресации из ячейки A20.

Скопируем закон преобразования информации ячейки B20 до ячейки B37 включительно.

Заметим, что в узлах интерполяции x = 1, 3, 5, 8 значения интерполяционного полинома P₃(x) точно соответствуют значениям исходной таблицы Y = 3, 10, 2, 5.

Равенство значений исходной таблицы и значений интерполяционного полинома P₃(x) в узлах интерполяции является доказательством правильности полученного решения.

Построим график интерполяционного полинома P₃(x), рис. 3.1.2.

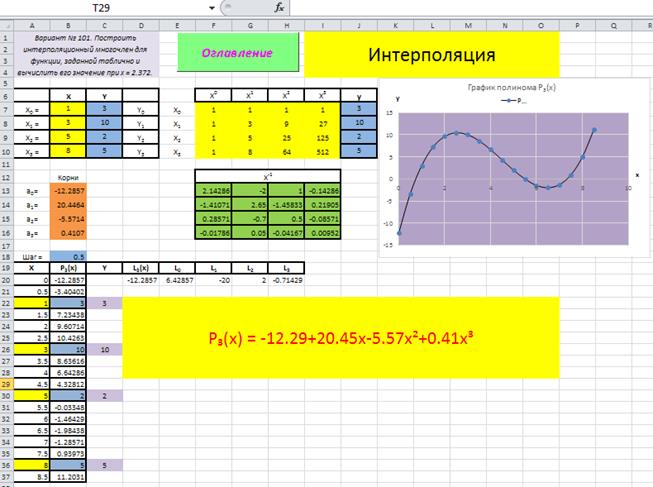
Рис. 3.1.2

Скопируем значения Y интерполяционной таблицы в столбец C таблицы табулирования интерполяционного полинома P₃(x), то есть C22 = C7, C26 = C8, C30 = C9, C36 = C10.

Добавим значения диапазона ячеек C20:C37 на график интерполяционного полинома P₃(x), рис. 3.1.3.

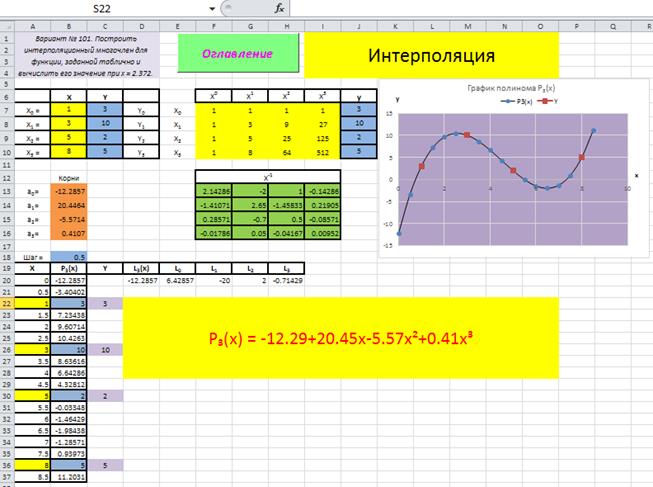
Рис. 3.1.3

Убедиться, что значения исходной таблицы Y в узлах интерполяции точно расположены по линии графика построенного интерполяционного полинома P₃(x).

Чтобы выполнить задание в полном объёме необходимо вычислить значение интерполяционного полинома P₃(x) при аргументе x = 2.372.

Для этого скопируем закон преобразования информации ячейки B37, соответствующий аналитическому выражению интерполяционного полинома P₃(x) = -12.29 + 20.45 x – 5.57 x² + 0.41 x³, например, в ячейку B39. То есть в ячейке B39запишется арифметическое выражение =$B$13+$B$14*A39^1+$B$15*A39^2+$B$16*A39^3.

В ячейку A39 внести константу 2.372, тогда в ячейке B39 отобразится результат вычисления значения интерполяционного полинома P₃(x) = 10.35, рис. 3.1.4.

Таким образом, задание выполнено:

– определено аналитическое выражение интерполяционного полинома P₃(x) = -12.29 + 20.45 x – 5.57 x² + 0.41 x³;

– вычислено значение интерполяционного полинома P₃(x)при x = 2.372,это значение равно 10.35.

Полученное значение P₃(x) = 10.35 достоверно, так значения интерполяционного полинома P₃(x) и исходной таблицы полностью совпадают в узлах интерполяции.

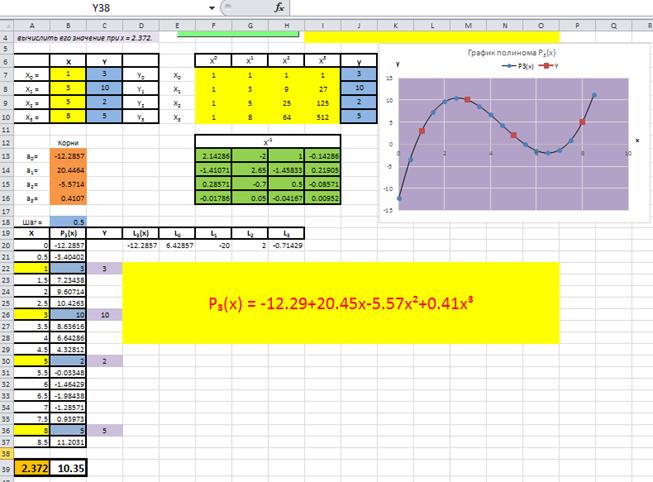
Рис. 3.1.4