Sub Horda2(a As Double, b As Double, delta As Double, c1 As Double, jj As Integer)

Dim c2 As Double

Fa = nel_ur_2(a)

Fb = nel_ur_2(b)

If Fa * Fb > 0 Then

MsgBox ("Интервал [a, b] выбран неправильно")

Exit Sub

End If

c1 = a - (b - a) / (Fb - Fa) * Fa

jj = 0

While Abs(c1 - c2) >= delta

Fa = nel_ur_2(a)

Fb = nel_ur_2(b)

Fc = nel_ur_2(c1)

If Fc * Fa > 0 Then b = c1: Fb = Fc Else a = c1: Fa = Fc

c2 = c1

c1 = a - (b - a) / (Fb - Fa) * Fa

jj = jj + 1

Wend

End Sub

Грамматические конструкции Subпозволяют, в отличие от грамматических конструкций Function, в списке формальных параметров задать несколько выходных параметров. Вызов грамматических конструкций Sub осуществляется с помощью специального оператора вызова Call.

Поэтому в объекте CommandButton1 пользовательской формы UserForm2 Решение нелинейных уравнений следует написать следующий программный модуль:

Private Sub CommandButton1_Click()

Dim a As Double, Ad As Double, Bd As Double

Dim An As Double, Ah As Double, bh As Double

Dim b As Double

Dim e As Double

Dim c As Double

Dim x1 As Double

Dim cc As Double

Dim i As Integer

Dim it As Integer

Dim jt As Integer

a = CDbl(TextBox1)

b = CDbl(TextBox2)

e = CDbl(TextBox3)

Ad = a: Bd = b

An = a:

Ah = a: bh = b

If OptionButton1 Then

Call PolDel(Ad, Bd, e, c, i)

TextBox4 = Format(c, "0.0000000000")

TextBox5 = i

Call Newton(An, e, x1, it)

TextBox8 = Format(x1, "0.0000000000")

TextBox9 = it

Call Horda(Ah, bh, e, cc, jt)

TextBox10 = Format(cc, "0.0000000000")

TextBox11 = jt

End If

If OptionButton2 Then

Call PolDel2(Ad, Bd, e, c, i)

TextBox4 = Format(c, "0.0000000000")

TextBox5 = i

Call Newton2(An, e, x1, it)

TextBox8 = Format(x1, "0.0000000000")

TextBox9 = it

Call Horda2(Ah, bh, e, cc, jt)

TextBox10 = Format(cc, "0.0000000000")

TextBox11 = jt

End If

End Sub

Некоторые комментарии к программе:

– фрагмент программы

Ad = a: Bd = b

An = a:

Ah = a: bh = b

обеспечивает запоминание начальных значений промежутка, в котором обнаружен корень [a;b], так при вычислениях в первой, по порядку, вызванной процедуре PolDel эти параметры принимают изменённые значения и при вызове в следующей, по порядку, процедуре Newton количество итераций определяется неправильно.

Использование пользовательской формы позволяет изменять значения промежутка, в котором обнаружен корень [a;b] и точность вычислений.

Так при точности e = 0,000000001 можно убедиться в полном совпадении значений корней вычисленных методом дихотомии, методом Ньютона и методом хорд и представленных в формате до десяти знаков после десятичной точки

-1,7148059167.

При этом видно, что выбранная точность при использовании метода дихотомии достигается за 27 итераций, при использовании метода Ньютона – за 4 итерации и при использовании метода хорд – за 5 итераций.

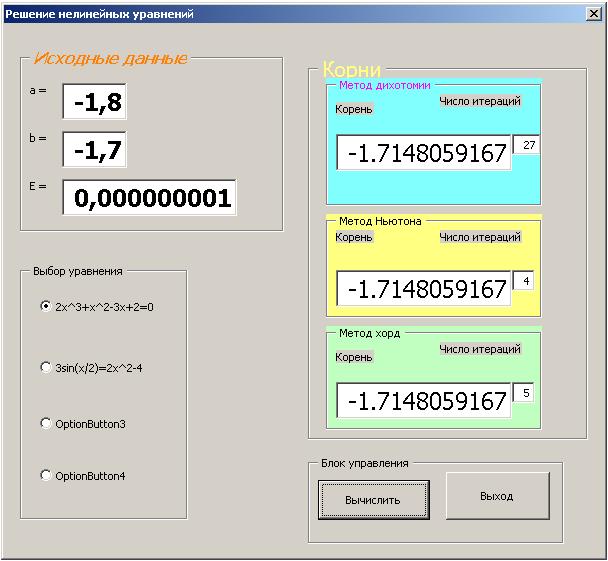
Рис. 2.5.2

Аналогичные результаты, с точки зрения совпадения значений корней, можно получить и для второго уравнения 3sin(x/2) = 2x² – 4, рис. 2.5.3.

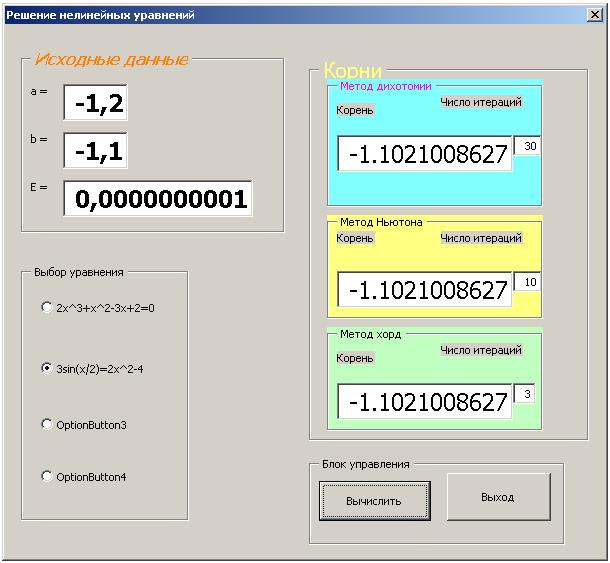
Рис. 2.5.3

С той только разницей, что совпадение значений корней до десятого разряда после десятичной точки произошло при точности e = 0, 0000000001и число итераций, обеспечивших это совпадение, при методе дихотомии – 30, при методе Ньютона – 10, а при методе хорд – 3.