Определение оператора Лапласа-Карсона

Пусть – комплекснозначная функция вещественной переменной t, удовлетворяющая условиям:

1) определена для всех

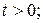
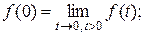
2) 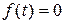при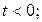

3) однозначна и непрерывна или кусочно-непрерывна при

Пусть 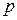– комплексное число;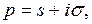 и - вещественные числа.

Определение 3.1. Оператором Лапласа-Карсона называется преобразование

(2.2)

Сокращенно это равенство записывают так: 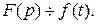Здесь - оригинал, 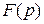- изображение. Интеграл Лапласа 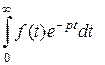может быть сходящимся или расходящимся. Потому возникает вопрос: для каких функций интеграл Лапласа сходится и преобразование Лапласа-Карсона имеет смысл?

Теорема 2.2

Если 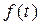– функция с ограниченным ростом, то при всех p таких, что 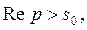где 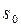– показатель роста , интеграл Лапласа сходится.

Доказательство

Обозначим 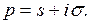Тогда

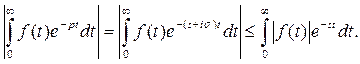
Этот интеграл по условию теоремы сходится при всех 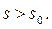Следовательно, и первый интеграл при всех p, для которых 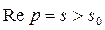, также сходится.

Во всех дальнейших рассуждениях, если не оговорено обратное, будем предполагать, что оригинал имеет ограниченный рост.