ГЛАВА 2. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
Линейные операторы и действия над ними
Пусть имеются два множества функций M и N.
Определение 2.1. Оператором над множеством функций M называется такое преобразование, которое каждой функции из множества М ставит в соответствие функцию из множества N .
Примеры операторов
Пример 1. Пусть М – множество функций, дифференцируемых n раз.
Нахождение первой производной – оператор над множеством функций М, обозначают его D или 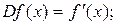
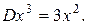
Нахождение второй производной – также оператор, обозначают его 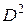 или
или 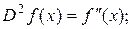
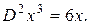
Нахождение n-й производной – оператор, обозначают его 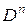 или
или
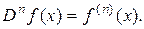
Пример 2. Однократное, двукратное, n-кратное интегрирование – операторы, для которых употребляются символы 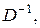
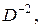 …
… 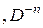 или
или
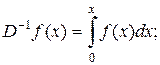
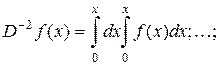
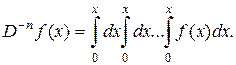
Пример 3. Пусть  – функция вещественного аргумента
– функция вещественного аргумента 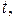
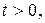
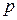 – комплексное число;
– комплексное число; 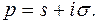 Если сходится
Если сходится 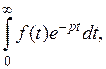 то он является некоторой функцией аргумента p:
то он является некоторой функцией аргумента p: 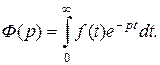
Интеграл, стоящий справа, называется интегралом Лапласа. Преобразование, по которому функции  ставится в соответствие функция
ставится в соответствие функция 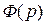 , называется преобразованием или интегральным оператором Лапласа.
, называется преобразованием или интегральным оператором Лапласа.
Пример 4. Пусть 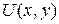 дважды дифференцируемая функция и
дважды дифференцируемая функция и
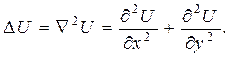
Преобразование, по которому функции U ставится в соответствие функция 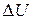 , называется дифференциальным оператором Лапласа.
, называется дифференциальным оператором Лапласа.
Дата добавления: 2020-07-18; просмотров: 528;











