Функции с ограниченным ростом
Пусть  – комплекснозначная функция вещественного аргумента t; т.е.
– комплекснозначная функция вещественного аргумента t; т.е. 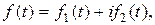 где
где 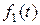 и
и 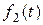 - вещественнозначные функции вещественного аргумента
- вещественнозначные функции вещественного аргумента 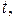
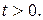 Рассмотрим интеграл
Рассмотрим интеграл
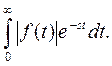 (2.1)
(2.1)
Допустим, что есть такое вещественное число s, что интеграл 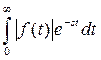 сходится. Тогда он сходится и при любом
сходится. Тогда он сходится и при любом 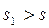 . Действительно, так как
. Действительно, так как
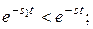
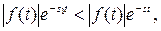 то
то 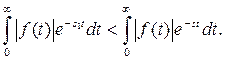
Интеграл, стоящий справа, сходится по условию. Интеграл, стоящий слева, берется от неотрицательной функции и мажорируется сходящимся интегралом, поэтому он тоже сходится.
Исходя из этого логически возможны три случая:
1) Найдется такое число 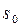 , что при всех
, что при всех 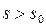 интеграл (2.1) сходится, а при
интеграл (2.1) сходится, а при 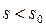 расходится.
расходится.
2) Интеграл сходится при всех s, т.е. 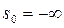 .
.
3) Интеграл расходится при всех s, т.е. 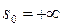 .
.
В первом и во втором случае говорят, что функция  имеет ограниченный рост,
имеет ограниченный рост, 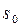 - показатель роста функции.
- показатель роста функции.
В третьем случае  называют функцией с неограниченным ростом.
называют функцией с неограниченным ростом.
Теорема 2.1
Если можно подобрать два такие положительные числа 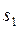 и M, что для любого
и M, что для любого 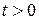
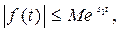 т.е. если
т.е. если 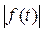 растет медленнее, чем некоторая экспоненциальная функция, то функция
растет медленнее, чем некоторая экспоненциальная функция, то функция  имеет ограниченный рост с показателем роста, меньшим
имеет ограниченный рост с показателем роста, меньшим 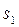 .
.
Доказательство
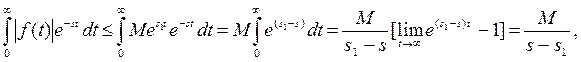
если 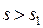 .
.
Итак, 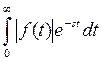 сходится при всех
сходится при всех 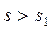 , следовательно,
, следовательно,  имеет ограниченный рост с показателем s0, s0 < s1.
имеет ограниченный рост с показателем s0, s0 < s1.
К функциям с ограниченным ростом относятся: 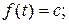
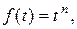
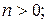
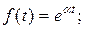
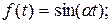
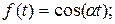
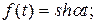
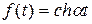 .
.
Примерами функций с неограниченным ростом являются:
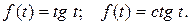
Дата добавления: 2020-07-18; просмотров: 651;











