Дифференциальные уравнения 1-го порядка.
Дифференциальное уравнение 1-го порядка связывает независимую переменную, искомую функцию и её первую производную:
f (x,y,y¢) = 0,
x - независимая переменная, y - искомая функция, y¢ - её производная.
y¢ = f (x,y) (32)
Уравнение (32) называется уравнением 1-го порядка, разрешённым относительно производной.
Решением дифференциального уравнения 1-го порядка называется всякая функция 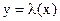 которая при подстановки в уравнение обращается в тождество.
которая при подстановки в уравнение обращается в тождество.
Общим решением дифференциального уравнения 1-го порядка 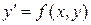 в области D называется функция
в области D называется функция 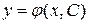 , обладающая следующими свойствами:
, обладающая следующими свойствами:
1) она является решением данного уравнения при любых значениях производной постоянной C, принадлежащей некоторому множеству;
2) для любого начального условия 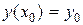 :
: 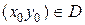 , существует единственное значение С = С0, при котором решение
, существует единственное значение С = С0, при котором решение 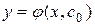 удовлетворяет заданному начальному условию.
удовлетворяет заданному начальному условию.
Всякое решение 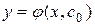 , получающееся из общего решения
, получающееся из общего решения 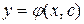 при конкретных значениях
при конкретных значениях 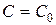 , удовлетворяющее заданному начальному условиюанному решение ну данного уравнения при егральной кривой надо задать (ьных кривых, го уравнения.
, удовлетворяющее заданному начальному условиюанному решение ну данного уравнения при егральной кривой надо задать (ьных кривых, го уравнения.
оизводную:
называется частным решением.
Дифференциальные уравнения с разделяющимися переменными Дифференциальное уравнение 1-го порядка называется уравнением с разделяющимися переменными, если его можно представить
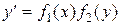 (33)
(33)
Метод интегрирования уравнения с разделяющимися переменными состоит в следующем: перепишем уравнение (33) в виде 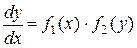 . Умножим обе части данного уравнения на
. Умножим обе части данного уравнения на 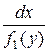 , получим:
, получим:
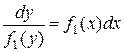 . (34)
. (34)
Если уравнение (33) представлено в виде (34), то говорят, что в нём разделены переменные. Интегрируя его, получим:
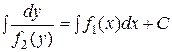 (35)
(35)
Выражение (35) представляет собой общий интеграл уравнения (4). Замечание. Разделив обе части уравнения (33) на 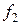 (y), мы можем потерять те решения, при которых
(y), мы можем потерять те решения, при которых 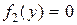 . Действительно, если
. Действительно, если 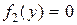 при
при 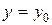 , то функция const
, то функция const 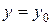 - является решением (33).
- является решением (33).
Пример № 81.Решить уравнение 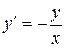 , y (1) = 2.
, y (1) = 2.
Решение. Запишем уравнение в виде: 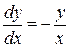 , разделяя переменные получим:
, разделяя переменные получим: 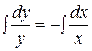 , интегрируя, находим общее решение
, интегрируя, находим общее решение 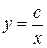 . При делении на yмы могли потерять решение y = 0, но последнее содержится в общем решении при С = 0.
. При делении на yмы могли потерять решение y = 0, но последнее содержится в общем решении при С = 0.
Однородные уравнения. Дифференциальное уравнение 1-го порядка называется однородным если его можно представить в виде:
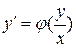 , (36)
, (36)
где правая часть есть функция только отношения 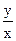 .
.
Введём новую функцию z , полагая 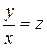 , или y = x×z, тогда у¢ = х¢×z + x×z¢. Подставляя в (36), получаем:
, или y = x×z, тогда у¢ = х¢×z + x×z¢. Подставляя в (36), получаем:
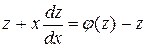 .
.
Предполагая, что 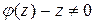 , имеем
, имеем 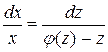 .
.
Интегрируя, получим:
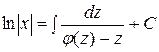 .
.
Возвращаясь к старой переменной y = x×z, получим искомое решение однородного уравнения.
Пример № 82. Решить дифференциальное 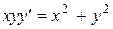 .
.
Решение. Убеждаемся, что данное уравнение является однородным:
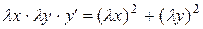 или
или 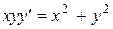 . Введём новую функцию z , полагая
. Введём новую функцию z , полагая 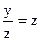 , или y = x×z, тогда у¢ = х¢×z + x×z¢. Подставляя в уравнение получим: х×xz× (х¢×z + x×z¢) = x2 + (xz)2. Сокращая на х2 приходим к уравнению:
, или y = x×z, тогда у¢ = х¢×z + x×z¢. Подставляя в уравнение получим: х×xz× (х¢×z + x×z¢) = x2 + (xz)2. Сокращая на х2 приходим к уравнению: 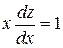 . Разделяя переменные и интегрируя, получим:
. Разделяя переменные и интегрируя, получим:
z = ln 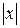 +C, или
+C, или 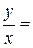 ln
ln 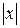 +C.
+C.
Линейные уравнения. Дифференциальное уравнение 1-го порядка называется линейным, если его можно представить в виде:
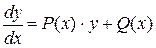 , (37)
, (37)
где P(x), Q(x) - заданные функции. Если Q(x) º 0, то уравнение (37) называется линейным однородным уравнением. Уравнение (37) интегрируется следующими способами.
1. Метод Лагранжа.
Решаем однородное уравнение, то есть уравнение 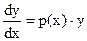 .
.
В этом уравнение переменные разделяются 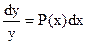 и его общее решение имеет вид:.
и его общее решение имеет вид:.
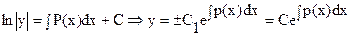
Общее решение будем искать в виде :
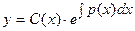 (38)
(38)

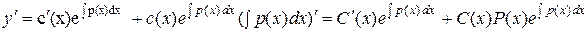 .
.
 Подставляем y и y¢ в уравнение (37):
Подставляем y и y¢ в уравнение (37):
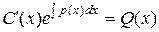 , или
, или 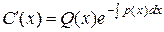 .
.
Интегрируя находим:
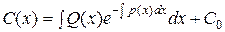
Подставляя найденное выражение в (38), получаем:
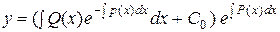
2. Метод Бернулли.
Решение уравнения (37) будем искать в виде:
у = u(x)×v(x).
Тогда уравнение (37) имеет вид:
(u(x)×v(x))¢ = Р(х) u(x)×v(x) + Q(x)
или
u¢(x)×v(x) + u(x)×v¢(x) - Р(х) u(x)×v(x) = Q(x).
Выберем в качестве v какое - нибудь частное решение уравнения:
v¢(x) - Р(х) ×v(x) = 0,
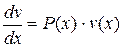 ,
,
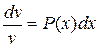 , откуда ln
, откуда ln 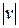 =
= 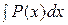 , или v =
, или v = 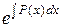 .
.
Тогда для отыскания u получим уравнение
u¢(x) 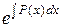 = Q(x).
= Q(x).
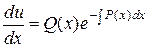 ,
,
откуда 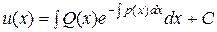 , значит общее решение данного уравнения имеет вид:
, значит общее решение данного уравнения имеет вид: 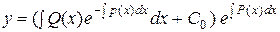 .
.
Пример № 83. Найти общее решение уравнения 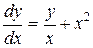 .
.
Решение. Решим методом Лагранжа.
1. Находим вначале решение однородного уравнения 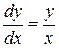 . Разделяя переменные и интегрируя, находим: ln
. Разделяя переменные и интегрируя, находим: ln 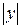 = ln
= ln 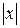 + C или у = Сх.
+ C или у = Сх.
2. Решение неоднородного уравнения ищем в виде: у = С(х)×х. Подставляем в уравнение данную функцию: С¢(х)×х + С(х) = С(х) + х2 или С¢(х) = х, проинтегрируем последнее уравнение: С(х) = 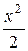 + А. Следовательно, общее решение уравнения имеет вид: у = (
+ А. Следовательно, общее решение уравнения имеет вид: у = ( 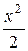 + А)×х.
+ А)×х.
Уравнения в полных дифференциалах. Рассмотрим дифференциальное уравнение
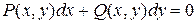 (39)
(39)
Это уравнение 1-го порядка, т.к. 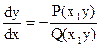 . Допустим, что
. Допустим, что 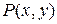 ,
, 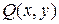 - непрерывны вместо со своими частными произв.
- непрерывны вместо со своими частными произв. 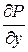 и
и 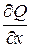 в некоторой области G. Если левая часть уравнения (39) является полным дифференциалом некоторой функции
в некоторой области G. Если левая часть уравнения (39) является полным дифференциалом некоторой функции 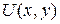 , т.е.
, т.е. 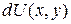 =
=
= 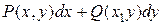 , то уравнение (39) называется уравнением в полных дифференциалах и может быть записано в виде
, то уравнение (39) называется уравнением в полных дифференциалах и может быть записано в виде 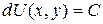 . Как известно, для того чтобы выражение Рdx + Qdy было полным дифференциалом необходимо чтобы в области G выполнялось равенство
. Как известно, для того чтобы выражение Рdx + Qdy было полным дифференциалом необходимо чтобы в области G выполнялось равенство
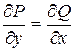 (40)
(40)
Если это условие выполняется, то функция 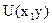 находится следующим образом:
находится следующим образом:
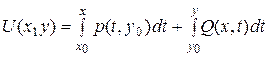 Þ
Þ
общий интеграл уравнения (39) запишем в виде:
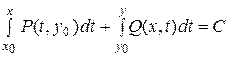
где - (х0; у0) произвольная фиксированная точка области G.
Пример 84. Проинтегрировать уравнение 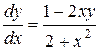 .
.
Решение. Итак, Р(х,у) = 2ху - 1, Q(х,у) = 2 + х2, тогда 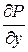 = 2х,
= 2х,
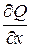 =2х, то есть выполнено условие (40). Следовательно,
=2х, то есть выполнено условие (40). Следовательно,
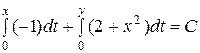 , -х + (2 + х2)у = С.
, -х + (2 + х2)у = С.
Дата добавления: 2020-07-18; просмотров: 706;











