Дифференциальные уравнения второго порядка.
Уравнение 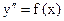 .Введём новую переменную
.Введём новую переменную 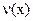 , полагая
, полагая 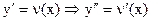 и, мы получим уравнение 1-го порядка:
и, мы получим уравнение 1-го порядка: 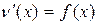 . Решая его имеем:
. Решая его имеем: 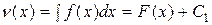 , где F(x) – одна из первообразных от f(x), т.к.
, где F(x) – одна из первообразных от f(x), т.к. 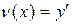 , то
, то
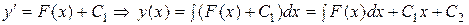
Уравнение 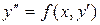 . Это уравнение не содержит явно искомой функции y. Введём новую переменную
. Это уравнение не содержит явно искомой функции y. Введём новую переменную 
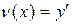 и, замечая, что
и, замечая, что 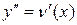 , получаем уравнение:
, получаем уравнение: 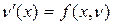 . Допустим, что найдено общее решение этого уравнения
. Допустим, что найдено общее решение этого уравнения 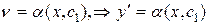 , то общее решение имеет вид:
, то общее решение имеет вид:
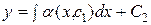 .
.
Пример 85. 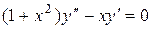 .
.
Решение. Это уравнение не содержит явно искомой функции y. Введём новую переменную 
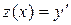 и замечая, что
и замечая, что 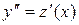 , получаем уравнение: (1+х2)z¢ - xz = 0 - уравнение первого порядка с разделяющимися переменными. Решая его, находим
, получаем уравнение: (1+х2)z¢ - xz = 0 - уравнение первого порядка с разделяющимися переменными. Решая его, находим 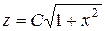 . Возвращаемся к старой переменной:
. Возвращаемся к старой переменной: 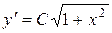 . Интегрируя, получим общее решение
. Интегрируя, получим общее решение 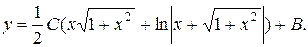
Уравнение вида 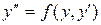 .Это уравнение не содержит явно независимую перемен. x. Введём новую переменную
.Это уравнение не содержит явно независимую перемен. x. Введём новую переменную 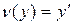 . Дифференцируем это равенство по x:
. Дифференцируем это равенство по x:
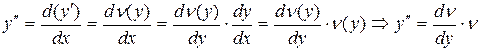 .
.
Тогда 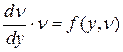 .Функция
.Функция 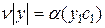 является общим решением этого уравнения. Учитывая, что
является общим решением этого уравнения. Учитывая, что 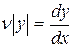 , получим уравнение с разделяющимися переменными:
, получим уравнение с разделяющимися переменными:
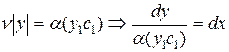 .
.
Интегрирую его получим общий интеграл:
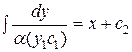 .
.
Пример 86.Решить уравнение 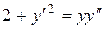 .
.
Решение. Это уравнение не содержит явно независимую перемен. x. Введём новую переменную 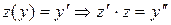 . Тогда получим уравнение с разделяющимися переменными: 2 + z2 = y×z×z¢, решая его находим
. Тогда получим уравнение с разделяющимися переменными: 2 + z2 = y×z×z¢, решая его находим 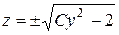 Þ
Þ 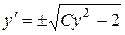 Þ
Þ 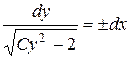 . Таким образом, общее решение имеет вид:
. Таким образом, общее решение имеет вид: 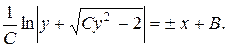
Линейные дифференциальные уравнения II порядка с постоянными коэффициентами.Линейные однородные дифференциальные уравнения II - го порядка с постоянными коэффициентами
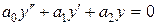 , (41)
, (41)
где 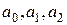 - const,
- const, 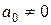 . Разделим уравнение (41) на а0 и введем обозначения
. Разделим уравнение (41) на а0 и введем обозначения 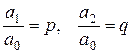 , получим уравнение:
, получим уравнение:
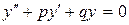 (42)
(42)
Уравнение к2 + рк +q = 0 называют характеристическим уравнением.
Характеристическое уравнение является уравнением второй степени, поэтому имеет два корня.
1) Корни характеристического уравнения действительные и различные: 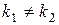 . В этом случае общее решение уравнения (41) имеет вид:
. В этом случае общее решение уравнения (41) имеет вид:
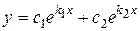
2) Корни характеристического уравнения равные: 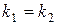 .
.
Тогда общее решение однородного линейного уравнения имеет вид:
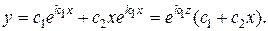
3) Корни характеристического уравнения комплексные.
Общее решение имеет вид:
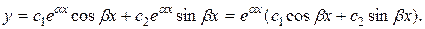
Пример 87. Найти общее решение уравнения. 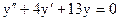 .
.
Решение. Составляем характеристическое уравнение: к2 + 4к +13 = 0, корни которого к1,2 = - 2 ± 3i. Следовательно, общее решение имеет вид: 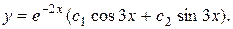
Линейные неоднородные дифференциальные уравнения IIго порядка с постоянными коэффициентами:
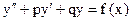 (43) ,
(43) ,
где 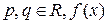 - функция. Общее решение (43) представляет собой сумму общего решения однородного уравнения и частного решения неоднородного уравнения.
- функция. Общее решение (43) представляет собой сумму общего решения однородного уравнения и частного решения неоднородного уравнения.
Для нахождения частного решения неоднородного уравнения применяют:
1) метод вариации пост.
2) метод подбора правой части.
Рассмотрим второй метод.
I. Правая часть уравнения 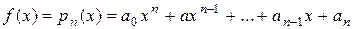 .
.
В этом случае частное решение 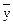 следует искать в виде:
следует искать в виде:

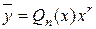 ,
,
где 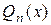 - многочлен той же степени, что и
- многочлен той же степени, что и 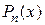 , с неизвестными коэффициентами, а r – число корней характеристического уравнения совпавших с нулем.
, с неизвестными коэффициентами, а r – число корней характеристического уравнения совпавших с нулем.
II. Правая часть уравнения 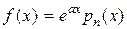 .
.
Частное решение 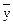 ищем в виде:
ищем в виде:
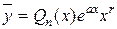 ,
,
где 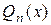 - многочлен с неопределенными коэффициентами степени n,
- многочлен с неопределенными коэффициентами степени n,
r - число корней характеристического уравнения, совпавших с коэффициентом 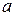 .
.
III. Правая часть уравнения 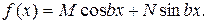
Тогда 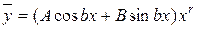 , где A, B – неизвестные коэффициенты,
, где A, B – неизвестные коэффициенты,
r - ровно числу корней характеристического уравнения совпавших с bi.
Теорема. Если 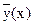 - частное решение линейное неоднородного уравнения (43), а У(x) – общее решение соответствующего однородного уравнения (41), то функция
- частное решение линейное неоднородного уравнения (43), а У(x) – общее решение соответствующего однородного уравнения (41), то функция 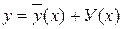 - является общим решением неоднородного уравнения (43).
- является общим решением неоднородного уравнения (43).
Пример 88.Найти общее решение уравнения 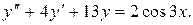
Решение. Общее решение однородного уравнения было найдено в примере 90: 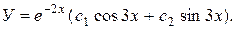 Частное решение неоднородного будем искать в виде:
Частное решение неоднородного будем искать в виде:
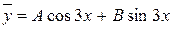 , ,
| |
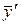 = = 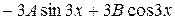 , ,
| |
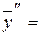 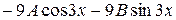
|
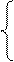 13
13 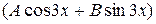 +4(
+4( 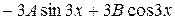 )
) 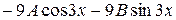 =
= 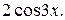
cos3x: 13А+12В - 9А = 2,
sin3x: 13В - 12А - 9В = 0, А = 1/20, В = 3/20.
Таким образом, 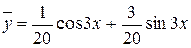 , а общее решение имеет вид
, а общее решение имеет вид 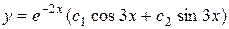
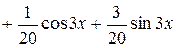 .
.
Дата добавления: 2020-07-18; просмотров: 608;











