Модуль 13. Элементы теории функции комплексного переменного.
Комплексные числа.
Комплексным числом α называется пара действительных чисел a и b, взятых в определённом порядке: 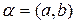 .
.
Рассмотрим число, изображаемой парой (0;1) – его обозначим через i. Тогда 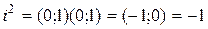 ,
, 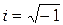 , всякое комплексное число может быть записано в виде:
, всякое комплексное число может быть записано в виде:
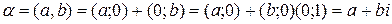
 | |||
 |
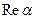
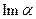
Очевидно, что если 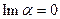 , то комплексное число
, то комплексное число 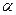 обращается в действительное число, если
обращается в действительное число, если 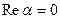 , в чисто мнимое. Два комплексных числа, по определению, называются равными, если равны между собой их действительные части и равны их мнимые.
, в чисто мнимое. Два комплексных числа, по определению, называются равными, если равны между собой их действительные части и равны их мнимые.
Два комплексных числа имеющих одну и ту же первую компоненту, но противоположные по знаку вторые компоненты, называются сопряжёнными и обозначаются 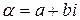 ,
, 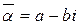 .
.
Сложение двух комплексных чисел α и β определим с помощью равенств: 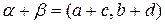 . Умножение двух комплексных чисел α и β определим с помощью равенства:
. Умножение двух комплексных чисел α и β определим с помощью равенства: 
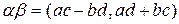 . Для нахождения частного двух комплексных чисел, заданных в алгебраической форме. Следует числитель и знаменатель умножить на число, сопряженное с делителем:
. Для нахождения частного двух комплексных чисел, заданных в алгебраической форме. Следует числитель и знаменатель умножить на число, сопряженное с делителем: 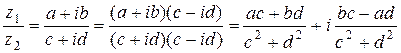 .
.
Всякое комплексное число 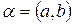 мы можем изображать на плоскости с координатами a и b.
мы можем изображать на плоскости с координатами a и b.
 y
y

 α
α
b
0 a x
Ось абсцисс называется действительной осью, ось ординат – мнимой осью. Плоскость, точки которой изображают комплексные числа, называют комплексно-числовой плоскостью.
Модулем комплексного числа α называют положительное число r 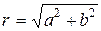 и обозначают через
и обозначают через 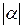 . Направление вектора α определяется с помощью угла j положительным направлением оси Ox и направлением этого вектора
. Направление вектора α определяется с помощью угла j положительным направлением оси Ox и направлением этого вектора 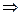 j изображает угол на который нужно повернуть «+» направление оси Ox, чтобы совпало с направлением вектора α. Это число j называется аргументом комплексного числа α и обозначается через
j изображает угол на который нужно повернуть «+» направление оси Ox, чтобы совпало с направлением вектора α. Это число j называется аргументом комплексного числа α и обозначается через 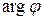 . Очевидно, что
. Очевидно, что 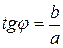 , так как r и j являются полярными координатами точки
, так как r и j являются полярными координатами точки 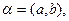 то имеем:
то имеем: 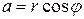 ,
, 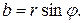
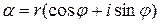 - тригонометрическая форма комплексного угла,
- тригонометрическая форма комплексного угла,
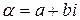 - алгебраическая форма комплексного числа.
- алгебраическая форма комплексного числа.
Теоремы о модуле и аргументе. Произведение двух комплексных чисел 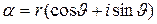 ,
, 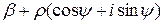 имеет вид:
имеет вид:
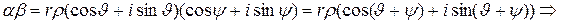
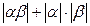 ,
, 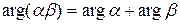 . Это равенство легко распространяется на случай n сомножителей
. Это равенство легко распространяется на случай n сомножителей 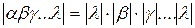 ;
; 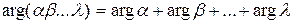 . А, следовательно,
. А, следовательно,
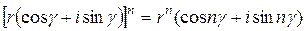 ,
,
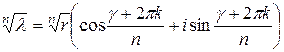 , k = 0, 1, 2,...,n -1.
, k = 0, 1, 2,...,n -1.
Геометрически эти n значений выражения 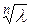 , очевидно, изображаются вершинами некоторого правильного n - угольника, вписанного в окружность, с центром в нулевой точке, радиуса
, очевидно, изображаются вершинами некоторого правильного n - угольника, вписанного в окружность, с центром в нулевой точке, радиуса 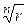 .
.
Аналогично, 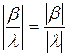 ,
, 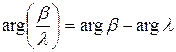 .
.
Пример 89. Представить число z =  в тригонометрической форме.
в тригонометрической форме.
Решение. Находим модуль комплексного числа: 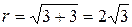 , находим значение аргумента:
, находим значение аргумента: 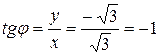 , так как Re z > 0, а Im z < 0, то j =
, так как Re z > 0, а Im z < 0, то j = 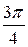 . Следовательно, тригонометрическая форма имеет вид: z =
. Следовательно, тригонометрическая форма имеет вид: z = 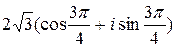 .
.
Пример 90. Найти 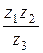 , если z1 = 1+5i, z2 = 3 - i, z3 = 2 +3i.
, если z1 = 1+5i, z2 = 3 - i, z3 = 2 +3i.
Решении: z1z2 = (1+5i)(3 - i ) = 3 - i + 15i - 5i2 = 8 -14i, 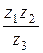 =
= 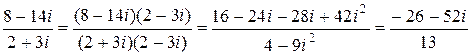 =
= 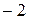 -4i.
-4i.
Пример 91. Решить уравнение w3 + 2i = 0.
Решение. Перепишем уравнение в виде w3 = -2i. Число -2i представим в тригонометрической форме: w3 = 2(cos 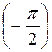 +i sin
+i sin 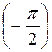 ), или
), или
w = 2 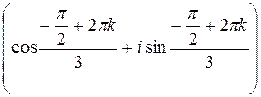 .
.
Если к = 0, то w0 = 2 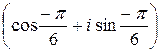 = 2
= 2 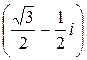 =
= 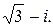
Если к = 1, то w1 = 2 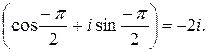
Если к = 2, то w2 = 2 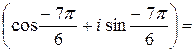 2
2 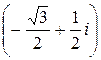 =
= 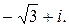
Дата добавления: 2020-07-18; просмотров: 573;











