Понятие функции комплексного переменного.
Даны две плоскости комплексных чисел 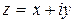 и
и 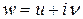 .
.


 у v
у v
| |||
 | |||
 0 х 0 u
0 х 0 u
Рассмотрим некоторое множество D в плоскости z и множество G в плоскости w. Если каждому числу 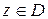 ставится в соотношении по некоторому закону определённое комплексное число
ставится в соотношении по некоторому закону определённое комплексное число 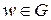 , то говорят, что на множестве D задана однозначная функция комплексной переменной, отображённое множество D в множество G и обозначается
, то говорят, что на множестве D задана однозначная функция комплексной переменной, отображённое множество D в множество G и обозначается 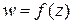 . Множество D называется областью определения функции.
. Множество D называется областью определения функции.
Функцию 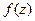 можно записать в виде
можно записать в виде 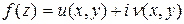 , где
, где 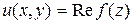 ,
, 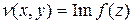 - действительные функции от переменных x,y.
- действительные функции от переменных x,y.
Если каждому значению z соответствует несколько разных значений w, то функция 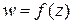 называется многозначной.
называется многозначной.
Говорят, что функция 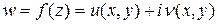 имеет предел в точке
имеет предел в точке 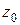 , равный числу
, равный числу 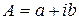 , если
, если 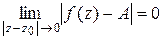 .
.
Для комплексных функций имеют место свойства, аналогичные соответствующим свойствам действительных функций:
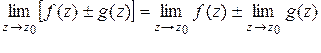
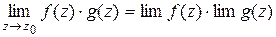 ;
;
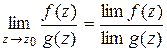 ,
, 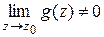
Функция 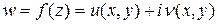 называется непрерывной в точке
называется непрерывной в точке 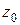 , если для неё выполняется свойство:
, если для неё выполняется свойство: 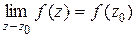
Это равенство эквивалентно двум равенствам:
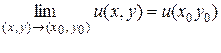
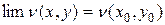 .
.
Следовательно, непрерывность f точке 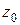 эквивалентно непрерывности функций
эквивалентно непрерывности функций 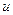 и
и 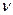 в точке
в точке 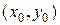 .
.
Производная функция комплексного переменного. Пусть задана однозначная функция 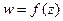 на области D комплексной плоскости z.
на области D комплексной плоскости z.
Производной от функции f(z) в точке z называется предел
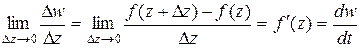 ,
,
когда 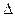 z любым образом стремиться к нулю.
z любым образом стремиться к нулю.
Функцию f(z), имеющую непрерывную производную в любой точке области D комплексной плоскости, называется аналитической функцией на этой области.
Основные свойства производных функций комплексных переменных, аналогичны соответствующим свойствам производных для функций действительных переменных.
Условия Коши – Римана. Рассмотрим комплексную функцию 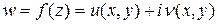 ,
, 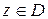 , определена на области D комплексной плоскости. Пусть она имеет производную в точке
, определена на области D комплексной плоскости. Пусть она имеет производную в точке 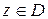 :
: 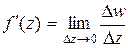 . Тогда следующие равенства называют условиями Коши - Римана:
. Тогда следующие равенства называют условиями Коши - Римана:
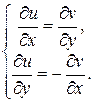
Теорема 1. Если функция 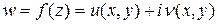 имеет производную в точке
имеет производную в точке 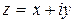 , то её действительные компоненты u и v d в точке (x,y) имеют частные производные 1-го порядка, удовлетворяющие условию Коши-Римана.
, то её действительные компоненты u и v d в точке (x,y) имеют частные производные 1-го порядка, удовлетворяющие условию Коши-Римана.
Теорема 2. Если функции u(x,y), v(x,y) имеют в точке (x,y) непрерывную частную производную, удовлетворяющую условие Коши-Римана, то её функция комплексная переменная 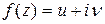 имеет в точке
имеет в точке 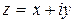 производную, которую можно вычислить по формуле:
производную, которую можно вычислить по формуле:
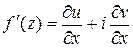 .
.
Теорема 3. Для того чтобы функция 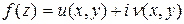 была аналитической на области D плоскости z, необходимо и достаточно чтобы частные произведения первого порядка функций u и v были непрерывны на D и выполнялось условие Коши-Римана:
была аналитической на области D плоскости z, необходимо и достаточно чтобы частные произведения первого порядка функций u и v были непрерывны на D и выполнялось условие Коши-Римана:
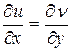 ;
; 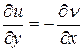 .
.
Формулы Эйлера. Рассмотрим ряд 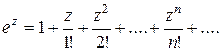
заменим в данном ряде z на iz ,тогда
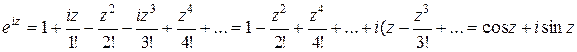 .
.


cos z sin z
так как 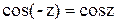 ,
, 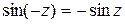 , то заменяя в тождестве Эйлера z на –z , получаем:
, то заменяя в тождестве Эйлера z на –z , получаем:
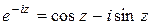 .
.
Из этих равенств можно получить следующие:
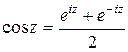 ,
, 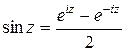
Эти формулы также носят название Эйлера.
Пользуясь тождеством Эйлера, получаем так называемую показательную формулу для представления  комплексного числа:
комплексного числа:
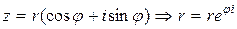
Пример 92. Дифференцируема ли функция f(z) = z2 - 2iz.
Решение: f(z) = (x+iy)2 -2i(x+iy) = x2 +2xyi -y2 -2xi + 2y = x2 - y2 +2y +
+ i(2xy - 2x), итак u = x2 - y2 +2y, v = 2xy - 2x, тогда
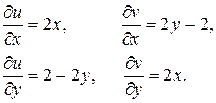
Условия Коши - Римана выполняются, следовательно, функция дифференцируема.
Дата добавления: 2020-07-18; просмотров: 584;











