Замена переменной в неопределенном интеграле

<1 234 5 6 7 >

Пусть х = j (t), где j (t) – монотонная, непрерывно дифференцируемая функция новой переменной t. Тогда формула замены переменной в этом случае имеет вид

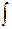f(x)dx = 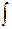f [j (t)] j¢ (t)dt .

Пример 46. Найти интеграл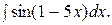

Решение:

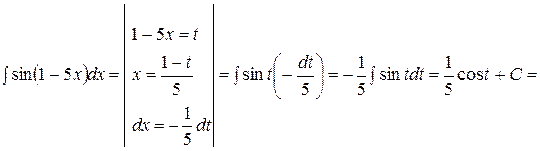
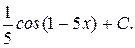
Пример 47. Найти интеграл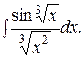

Решение:

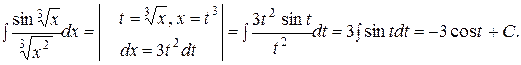
Ответ должен быть выражен через старую переменную 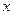. Подставляя в результат интегрирования 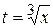, получим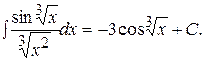

Пример 48. Найти интеграл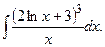

Решение:

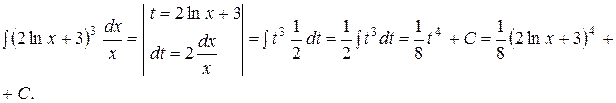Пример 49. Найти интеграл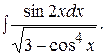

Решение:

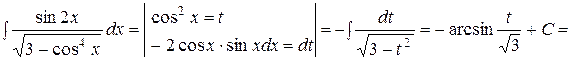
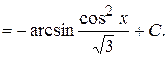
Пример 50. Найти интеграл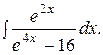

Решение:

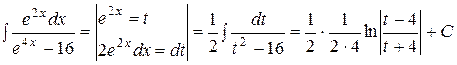. Возвращаясь к старой переменной, получим

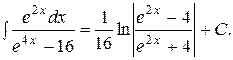
9.3. Интегрирование по частям

Интегрированием по частям называется нахождение интеграла по формуле

= – ,

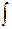
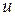
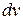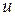
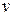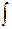
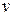
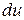где 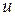= j(х), 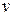= y (x) – непрерывно дифференцируемые функции от x.

При этом за u берется такая функция, которая при дифференцировании упрощается, а за dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.

Так, например, для интегралов вида

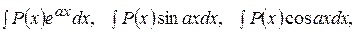
где 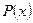- многочлен, за uследует принять 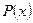, а за dv - соответственно выражение 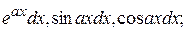для интегралов вида

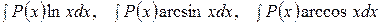
за u принимаются соответственно функции 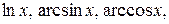а за dv - выражение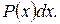

Пример 51. Найти интеграл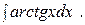

Решение:

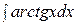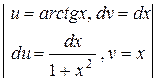= . По формуле интегрирования по частям находим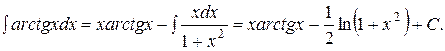

Пример 52. Найти интеграл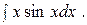

Решение:

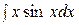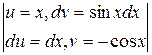= . Отсюда по формуле интегрирования по частям находим: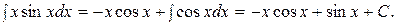

<1 234 5 6 7 >

Дата добавления: 2020-07-18; просмотров: 389;