Интегрирование рациональных функций
Дробной - рациональной функцией называется функция, равная частному от деления двух многочленов:
R(x) = 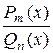 .
.
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, в противном случае - неправильной. Отметим, что всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби:
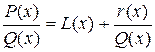 ,
,
где r(x) - многочлен, степени меньше степени знаменателя Q(x). Таким образом, интегрирование рациональной функции сводится к интегрированию правильной рациональной дроби. А интегрирование правильной рациональной дроби сводится к интегрированию простейших дробей типа:
1. 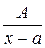 ; 2.
; 2. 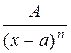 ;
;
3. 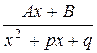 ; 4.
; 4. 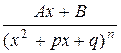 .
.
(x2 +рх + q - не имеет действительных корней.)
Интегрирование простейших рациональных дробей:
1. 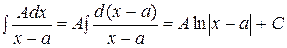 .
.
2. 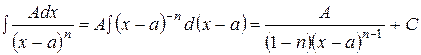 .
.
3. Основной способ нахождения интеграла 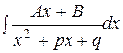 состоит в предварительном выделении полного квадратного трехчлена:
состоит в предварительном выделении полного квадратного трехчлена:
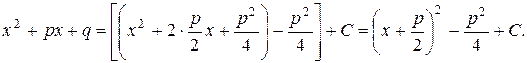
Рассмотрим этот способ на примере.
Пример 53. Вычислить интеграл 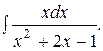
Решение. Выделим полный квадрат в знаменателе и преобразуем дробь:
х2 +2х -1 = х2 +2х +1-1-1 = (х+1)2 -2.
Тогда 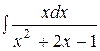 =
= 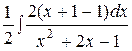 =
= 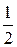
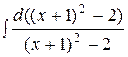 -
- 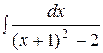 =
=
= 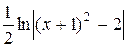 -
- 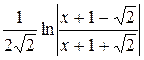 +С.
+С.
4. Если введем новую переменную t, положив t = х + 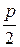 и
и
х2 + рх + q = t2 + a2, где a2 = q - 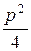 , то интеграл
, то интеграл 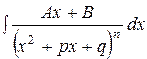 =In можно вычислить с помощью реккурентной формулы
=In можно вычислить с помощью реккурентной формулы
In = 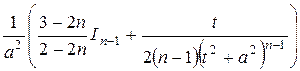 .
.
9.5. Интегрирование рациональных дробей с помощью разложения на простейшие дроби
Случай 1.Знаменатель имеет только действительные различные корни, т.е. разлагается на неповторяющиеся множители первой степени.
Пример 54. Найти интеграл 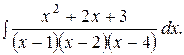
Решение. Так как каждый из двухчленов 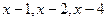 входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде
входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде
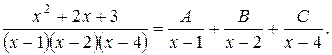
Освобождаясь от знаменателей, получим
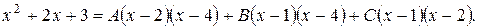
При х = 1 6 = 3А, А = 2;
при х = 2 11 = -2В, В= - 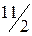 ;
;
при х = 4 27 = 6С, С = 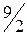 .
.
Итак, разложение рациональной дроби на простейшие имеет вид
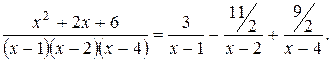
Таким образом,
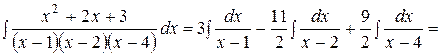
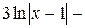
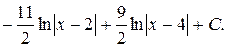
Случай 2. Знаменатель имеет лишь действительные корни, причем некоторые из них кратные, т.е. знаменатель разлагается на множители первой степени и некоторые из них повторяются.
Пример 55. Найти интеграл 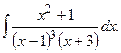
Решение. Множителю 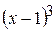 соответствует сумма трех простейших дробей
соответствует сумма трех простейших дробей 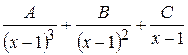 , а множителю
, а множителю 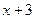 - простейшая дробь
- простейшая дробь 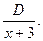 Итак,
Итак,
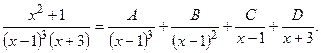
Освободимся от знаменателя:
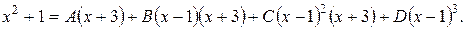
| х = 1 | 2 = 4А; A = 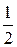
|
| x = -3 | 10 = -64D; D = - 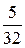
|
| x = 0 | 1= 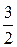 -3B + 3C + -3B + 3C + 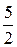
|
| x = -1 | 2 = 1- 4B + 8C + 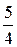
|
Откуда В = 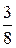 , С =
, С = 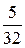 .
.
Окончательное разложение данной дроби на простейшие имеет вид
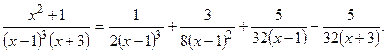
Таким образом, получим
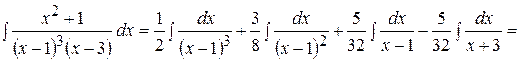
= 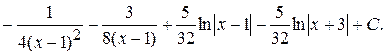
Случай 3. Среди корней знаменателя имеются простые комплексные корни, т.е. разложение знаменателя содержит квадратичные неповторяющиеся множители.
Пример 56. Найти интеграл 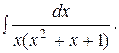
Решение. Разлагаем дробь на простейшие дроби
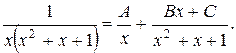
Освобождаемся от знаменателя:
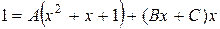 . Выпишем коэффициенты при одинаковых степенях:
. Выпишем коэффициенты при одинаковых степенях:
| при х2: | 0 = А+В |
| x: | 0 = A+C |
| x0: | 1 = A |
Откуда найдем А = 1, В = -1, С = -1.
Итак, 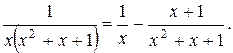
Следовательно,
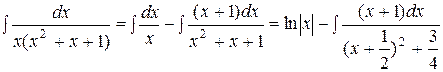 = ln|x|-
= ln|x|-
- 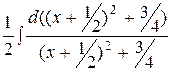 -
- 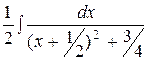 = ln|x| -
= ln|x| - 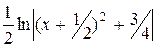 -
-
- 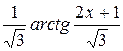 +C.
+C.
Случай 4. Среди корней знаменателя имеются кратные комплексные корни, т.е. разложение знаменателя содержит повторяющиеся квадратичные множители.
Пример 57. Найти интеграл 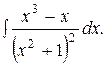
Решение. Так как 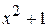 есть двукратный множитель, то
есть двукратный множитель, то
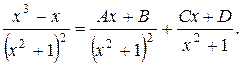
Освобождаясь от знаменателей, получим
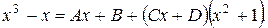
Приравняем коэффициенты при одинаковых степенях 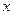 :
:
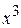
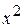
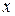 1 1
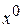
|
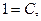
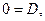
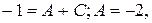
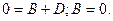
|
Следовательно,
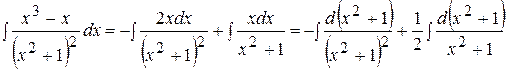 =
=
= 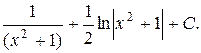
9.5. Интегрирование иррациональных функций
Неопределенный интеграл вида 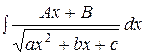 интегрируется
интегрируется
путем введения новой переменной 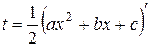 .
.
Интегралы вида 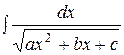 интегрируются путем выделения полного квадрата из квадратного трехчлена.
интегрируются путем выделения полного квадрата из квадратного трехчлена.
Пример 58. Вычислить интеграл 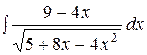 .
.
Решение:
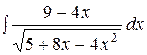 =
= 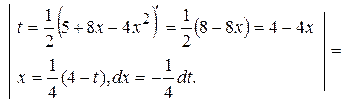
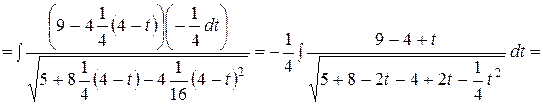
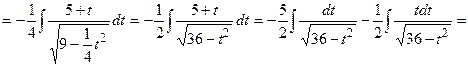
= 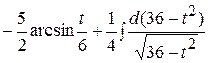
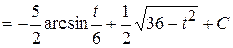 , где
, где 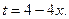
Пример 59. Вычислить интеграл 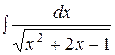 .
.
Решение:
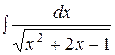 =
= 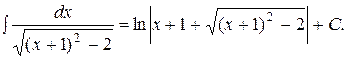
Интеграл вида 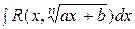 , где n Î Z, интегрируются путем введения новой переменной t n = ax + b.
, где n Î Z, интегрируются путем введения новой переменной t n = ax + b.
Пример 60. Вычислить интеграл 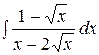 .
.
Решение:
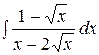 =
= 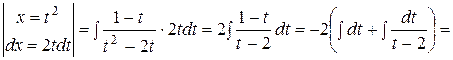
= -2t-2 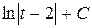 = -2
= -2 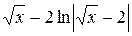 +С.
+С.
Интегралы вида 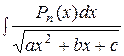 , где Pn (x) - многочлен степени n, вычисляются с помощью реккурентной формулы
, где Pn (x) - многочлен степени n, вычисляются с помощью реккурентной формулы
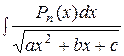 =
= 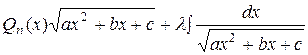 , (21)
, (21)
где Q n - 1 (x) - многочлен степени (n - 1) с неопределенными коэффициентами и l - число. Коэффициенты многочлена и число l находятся при помощи дифференцирования тождества (21).
Пример 61. Вычислить интеграл 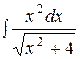 .
.
Решение. Применяем формулу (21):
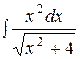 = (Ах+В)
= (Ах+В) 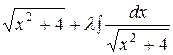 . Дифференцируем это тождество:
. Дифференцируем это тождество: 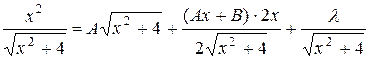 . Откуда
. Откуда
х2 = А(х2 + 4) + х(Ах+В) + l.
Выпишем коэффициенты при одинаковых степенях:
х2: 1 = А +А
х: 0 = Вх
х0: 0 = 4A + l.
Итак, А = 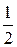 , В = 0, l = -2. Следовательно,
, В = 0, l = -2. Следовательно,
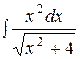 =
= 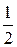
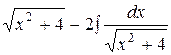 =
= 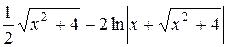 +С.
+С.
Интеграл от дифференциального бинома 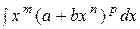 , где m, n, p - рациональные числа:
, где m, n, p - рациональные числа:
1) если р - целое число, то делаем замену х = t s, где s - общий знаменатель дробей m и n;
2) если 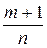 - целое число, то делаем замену а+bх n = t s, где s - знаменатель дроби р;
- целое число, то делаем замену а+bх n = t s, где s - знаменатель дроби р;
3) если 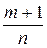 +р - целое число, то делаем замену ах – n+b = t s, где s - знаменатель дроби р.
+р - целое число, то делаем замену ах – n+b = t s, где s - знаменатель дроби р.
Пример 62. Вычислить интеграл 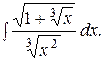
Решение:
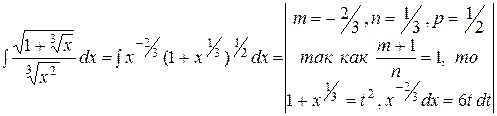 = =
= = 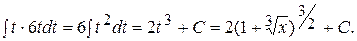
9.7. Интегрирование тригонометрических функций
1.Интегралы вида 
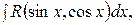 где R - рациональная функция, приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки
где R - рациональная функция, приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки 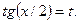 В результате этой подстановки имеем:
В результате этой подстановки имеем:
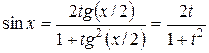 ;
;
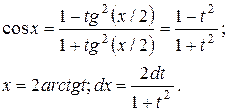
Пример 63. Найти интеграл 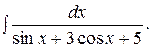
Решение. Введем новую переменную tg 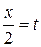 . Тогда
. Тогда 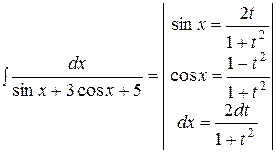 =
= 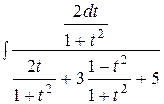 =
=
= 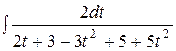 =
= 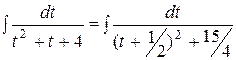 =
= 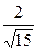 arctg
arctg 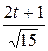 +
+
+C = 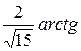
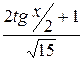 +C.
+C.
Универсальная подстановка 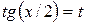 во многих случаях приводит к сложным вычислениям, так как при ее применении
во многих случаях приводит к сложным вычислениям, так как при ее применении 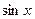 и
и 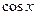 выражаются через
выражаются через 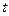 в виде рациональных дробей, содержащих
в виде рациональных дробей, содержащих 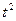 .
.
В некоторых частных случаях нахождение интеграла вида 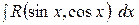 может быть упрощено:
может быть упрощено:
1. Если 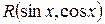 - нечетная функция относительно
- нечетная функция относительно 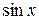 , т.е., если
, т.е., если 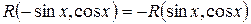 , то интеграл рационализируется подстановкой
, то интеграл рационализируется подстановкой 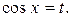
2. Если 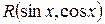 - нечетная функция относительно
- нечетная функция относительно 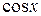 , т.е., если
, т.е., если 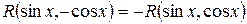 , то интеграл рационализируется с помощью подстановки
, то интеграл рационализируется с помощью подстановки 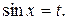
3. Если 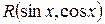 - четная функция и относительно
- четная функция и относительно 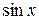 и относительно
и относительно 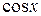 , т.е., если
, т.е., если 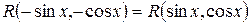 , то к цели приводит подстановка
, то к цели приводит подстановка 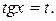
Пример 64. Найти интеграл 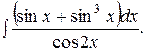
Решение. Так как подынтегральная функция нечетна относительно синуса, то полагаем 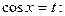
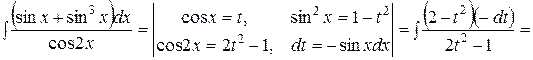
= 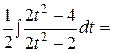
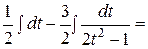
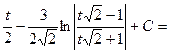
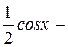
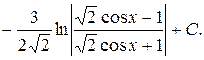
2. Интегралы вида 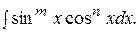
Выделим здесь два случая, имеющие особенно важное значение.
Случай 1. По крайней мере один из показателей m или n – нечетное положительное число.
Если n – нечетное положительное число, то применяется подстановка 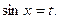 Если же m - нечетное положительное число, подстановка
Если же m - нечетное положительное число, подстановка 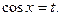
Пример 65. Найти интеграл 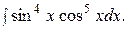
Решение. Полагая 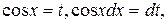 получим
получим
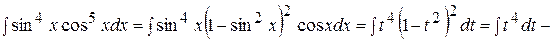
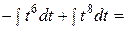
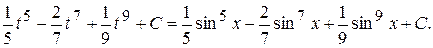

Случай 2. Оба показателя степени m и n - четные положительные числа. Здесь следует преобразовать подынтегральную функцию с помощью следующих формул:
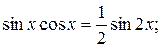 (22)
(22)
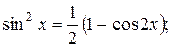 (23)
(23)
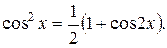 (24)
(24)
Пример 66. Найти интеграл 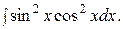
Решение. Из формулы (22) следует, что
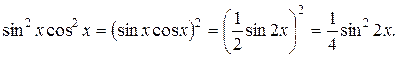 Применив теперь формулу (23), получаем
Применив теперь формулу (23), получаем 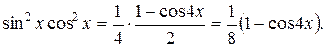
Итак, 
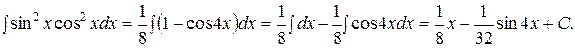
3. Интегралы вида 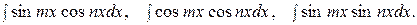
Тригонометрические формулы
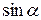
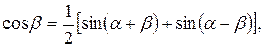
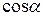
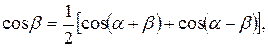
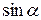
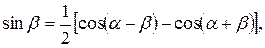
дают возможность произведение тригонометрических функций представить в виде суммы.
Дата добавления: 2020-07-18; просмотров: 908;











