Модуль 9. Векторный анализ
Скалярное и векторное поле. Если каждой точки М области V поставлено в соответствие некоторое число u(М) (некоторый вектор F(M)), то говорят что в V задано скалярное поле (векторное поле).
Если введены декартовы координаты, то понятие скалярного поля совпадает с понятием функции трех или двух переменных: u = u (x,y,z) или u = u (x,y), а в векторном поле F(M) можно представить как совокупность трех функций: F(M) = P(x,y,z)i + Q(x,y,z)j + R(x,y,z)k.
Производная по направлению.Для изучения поведения поля
z = ¦(x, y) в точке М0(x0, y0) в направлении вектора 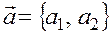 следует через М0 провести прямую с направляющим вектором
следует через М0 провести прямую с направляющим вектором 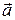 и исследовать функцию z(t) в точке М0 (т.е. при t = 0 характеризует скорость изменения поля в этой точке в направлении
и исследовать функцию z(t) в точке М0 (т.е. при t = 0 характеризует скорость изменения поля в этой точке в направлении 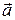 ). Если величину z ¢(0) разделить на
). Если величину z ¢(0) разделить на 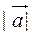 , то получим производную по направлению
, то получим производную по направлению 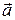 данного скалярного поля в данной точке:
данного скалярного поля в данной точке:
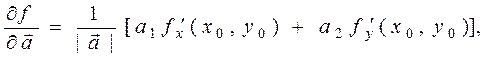
где 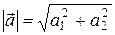 .
.
Вычисление производной по направлению производится с помощью следующей формулы:
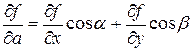 , где cos a, cos b - направляющие косинусы.
, где cos a, cos b - направляющие косинусы.
Градиент скалярного поля. Градиентом скалярного поля u(M) называют вектор
grad u = 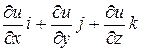 .
.
Величина grad u определяется формулой
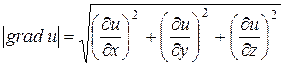 .
.
В декартовой системе координат производная по направлению вектора авычисляется по формуле
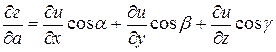 ,
,
a, b, g - углы, образованные вектором а с осями координат.
Если вектор а имеет направление grad u, то
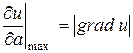 .
.
Пример 41.Дана функция z = xy2. Найти производную в точке
А (0,5;0,5) в направлении градиента функции.
Решение. Так как 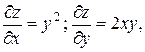 то
то 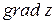 = y2i +2xyj, следовательно,
= y2i +2xyj, следовательно, 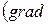
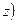 a=
a= 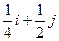 ;
; 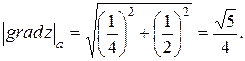
Направляющие косинусы градиента следующие: cos 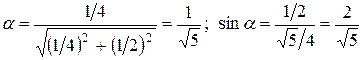 .
.
Следовательно, 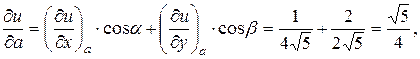 т.е.
т.е. 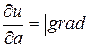
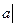 .
.
Пример 42. Дана функция z = xy. Найдем ее производную в точке Р ( 5, 1) в направлении от этой точки к точке Q (7, -1).
Решение. Находим частные производные функции z = xy и вычисляем их значения в точке Р:
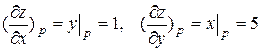 .
.
Так как вектор PQ имеет координаты {2,-2}, то |PQ| = 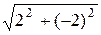 =
=
=2 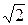 , а его направляющие косинусы
, а его направляющие косинусы 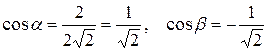 .
.
Следовательно, 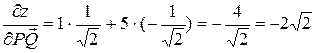 . Знак минус означает, что функция z в этом направлении убывает.
. Знак минус означает, что функция z в этом направлении убывает.
Пример 43.Найти величину и направление градиента скалярного поля z = x3 +y3 - 2xy в точке М0 (2,1).
Решение. Находим частные производные функции z:
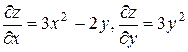 -2х, их значения в точке М0:
-2х, их значения в точке М0:
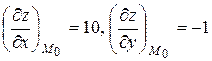 .
.
Получаем (grad z)M = 10i - j, а величина градиента 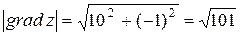 .
.
Дата добавления: 2020-07-18; просмотров: 540;











