Производная и дифференциал

Приращением функции z = ¦(x, y) в точке (x, y) называется величина

Dz = ¦(x + Dx, y + Dy) – ¦(x, y),

где Dx, Dy – приращения независимых переменных. Частными приращениями по x и по y называются соответственно величины:

D _хz = ¦(x + Dx, y) - ¦(x, y), D_yz = ¦(x, y + Dy) - ¦(x, y).

Частными производными функции z по x по y в точке (x, y) называются соответственно величины: 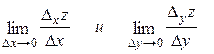(при условии, что эти пределы существуют). Для них приняты обозначения: .

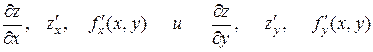Функция z = ¦(x, y) называются дифференцируемой в точке (x, y), если ее приращение в этой точке представимо в виде

Dz = A(x, y)Dx + B(x, y)Dy + o (r),

r = 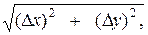где о (r) – величина более высокого порядка малости по сравнению с r при r®0 (т.е. о(r)/r®0 при r®0). В этом случае в точке (x, y) существуют частные производные, причем z¢_x =

= A(x, y), z¢_y = B(x, y). Обратно, если функция имеет в точке (x, y) непрерывные частные производные, то она дифференцируема в этой точке.

!Если рассмотреть многомерную функцию полезности u (x₁, x₂, …,x_n), то вектор составленный из частных производных функции полезности 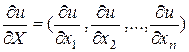называют вектором предельной полезности.

Дифференциалом функцииz = ¦(x, y) называется величина

dz = ¦¢_x(x, y)Dx + ¦¢_y(x, y)Dy. Полагая дифференциалы dx и dy независимых переменных равными соответственно Dх и Dу, имеем

dz = ¦¢_x(x, y)dx + ¦¢_y(x, y)dy.

Пример 38.Найти z¢_x, z¢_y от функции z = x²y-3xy⁴-1.

Решение. Считая у константой, имеем z¢_x = 2xy -3y⁴, считая х константой, имеем z¢_y = х² 12ху³.

Пример 39. Найти полный дифференциал функции z = 2xy - x²+y³.

Решение. Находим частные производные z¢_x, z¢_y:

z¢_x = 2y - 2x; z¢_y = 2x +3y². Тогда dz = 2(y - x)dx + (2x +3y²)dy.

Сложная функция.Пусть z = ¦(x, y), причем x = x(u, v), y =

= y(u, v). Пусть для (u, v) Î D функции x(u, v), y(u, v) принимают значения, при которых функция z = ¦(x, y) определена. Тем самым на множестве D задается функция z(u, v) = ¦(x(u, v), y(u, v)), которая называется сложной функцией; при этом функция ¦(x, y) называется внешней, а x(u, v), y(u, v) – внутренними функциями.

Частные производные сложной функции находятся по формулам:

Пусть z = z (t, x, y), причем x = x (t), y = y (t). Тогда z, в конечном счете, зависит только от t. Производная 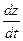вычисляется по формуле

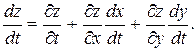
Пример 34. Найти z¢_t ,если z = e ^xy, x = sint, y = lnt.

Решение. В начале составляем формулу

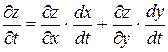Тогда 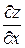= уе ^ху, 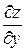= хе ^ху, х¢_t = cost, y¢_t = 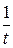. Следовательно,

z¢_t = уе ^ху cost+ хе ^ху 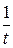= te ^sin^t(lnt×cost + ).

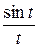Пример 35. Найти 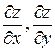, если z = sin(u+v), где u = x², v = y².

Решение. Так как 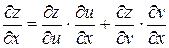, , 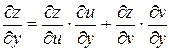то вычисляя частные производные

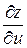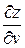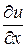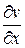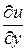= cos (u+v), = cos (u+v), = 2x, = 0, = 0, 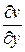= 2y, получаем 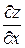= cos (u + v)×2х + cos (u + v)×0 = cos (x ²+y ²)×2x,

аналогично 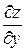= cos (x ²+y ²)×2у.

Вторые частные производные и вторые производные дифференциалы. Вторыми частными производнымифункции z = ¦(x, y) называются частные производные. Их обозначают так:

Производные z¢¢_xy и z¢¢_yx называется смешанными. Если в рассматриваемой точке смешанные производные непрерывны, то они равны в этой точке.

Аналогично определяются частные производные более высоких порядков.

Вторым дифференциалом функции z = ¦(x, y) называется выражение

d²z = d(dz) = (dz)¢_xDx + (dz)¢_yDy = z¢¢_xx(Dx)² + 2z¢¢_xyDxDy + z¢¢_yy(Dy)².

Аналогично определяются величины d ³z, d ⁴z и т.д.

Пример 36.Дана функция z = x³+ 2x²y - 8xy²+ y³. Найти ее частные производные второго порядка.

Решение. Находим сначала первые производные:

z¢_x= 3x²+ 4xy - 8y², z¢_y = 2x ²- 16xy + 3y ².

Пользуясь определениями и правилами дифференцирования, получаем z¢¢_xx = 6x + 4y, z¢¢_xy = 4x – 16y, z¢¢_yy = -16x + 6y.

Пример 37. Дана функция z = ln (x² + y² + 2x + 1). Показать, что z¢¢_xx + z¢¢_yy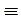0.

Решение. Найдем частные производные первого и второго порядка:

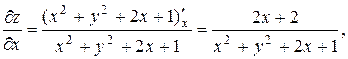
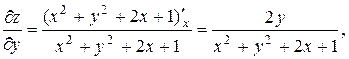
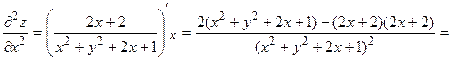
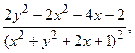
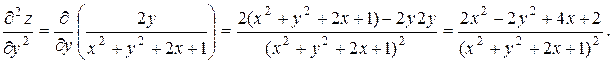Составив сумму z¢¢_xx + z¢¢_yy вторых частных производных, убедимся, что она тождественно равна нулю:

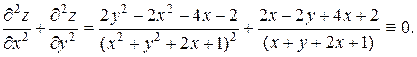
Неявные функции и их дифференцирование.Уравнение

F(x, y) = 0, имеющее решение (x₀, y₀), определяет в окрестности x₀ переменную y как непрерывную функцию x при условии, что производная F¢_y(x, y) ¹ 0 и непрерывна в некоторой окрестности точки (x₀, y₀). Если, кроме того, в окрестности этой точки существует непрерывная производная F¢_x, то неявная функция y = y(x) имеет производную, определяемую по формуле

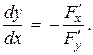
Рассмотрим теперь уравнение F(x, y, z) = 0, связывающие переменные x, y, z; при этом функция z = j(x, y) непрерывна и имеет непрерывные частные производные, которые определяются по формулам:

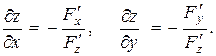
Пример 38.Найти частные производные функции

x²+ xsiny +2z + +e^z = 0.

Решение: F¢_x = 2x + siny; F¢_y = xcosy; F¢_z = 2 + e^z, тогда частные производные равны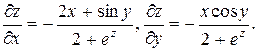

7.2. Экстремумы функций нескольких переменных

Точка (x₀, y₀) называется точкой минимума (максимума) функций z = ¦(x, y), если в некоторой окрестности точки (x₀, y₀) функция определена и удовлетворяет неравенству ¦(x, y) > ¦(x₀, y₀) (соответственно ¦(x, y) < ¦(x₀, y₀)). Точка максимума и минимума называются точками экстремума функции.

Необходимое условие экстремума. Если в точке экстремума функция имеет первые частные производные, то они обращаются в этой точке в нуль. Отсюда следует, что для отыскания точек экстремума такой функции z = ¦(x, y) следует решить систему уравнений ¦¢_x(x, y) = 0, ¦¢_y(x, y) = 0. Точки, координаты которых удовлетворяют этой системе, называются критическими точками функции. Среди них могут быть точки максимума, точки минимума, а также точки, не являющиеся точками экстремума.

Достаточные условия экстремума используются для выделения точек экстремума из множества критических точек и перечислены ниже.

Пусть функция z = ¦(x, y) имеет в критической точке непрерывные вторые производные. Если в этой точке выполняется условие

D = ¦¢¢_xx¦¢¢_yy – (¦¢¢_xy)² > 0,

то она является точкой минимума при ¦¢¢_xx > 0 и точкой максимума при

¦¢¢_xx < 0. Если в критической точке D < 0, то она не является точкой экстремума. В случае D = 0 требуется более тонкое исследование характера критической точки, которая в этом случае может быть точкой экстремума, а может и не быть таковой.

Пример 39.Найти экстремум функции

f (x, y) = x² + y² – 4x + 6y +17.

Решение. Находим частные производные f ¢_x = 2x – 4, f ¢_y = 2y + 6, f ²_xx = 2, f ²_xy = 0, f ²_yy = 2. Решаем систему

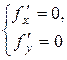или 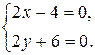Þ х = 2, у = -3.

Используя достаточные условия экстремума D = 2 × 2 - 0 = 4 > 0,

А = 2 > 0, делаем вывод, что точка М₀ (2, -3) - точка минимума, причем min f (x, y) = f (2, - 3) = 4.

Нахождение наибольшего и наименьшего значения. Для того чтобы найти наибольшее и наименьшее значение функции z= f(x,y) в замкнутой области, нужно:

1) найти все стационарные точки внутри этой области, вычислить значение функции в этих точках;

2) найти наибольшее и наименьшее значение функции на границе области;

3) из всех этих чисел выбрать соответственно наибольшее и наименьшее значение.

Пример 40.Найти наибольшее и наименьшее значения функции

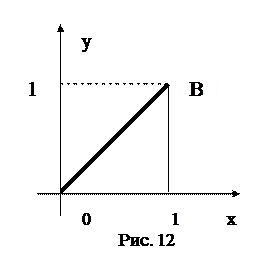
z = f (x, y) = 3 – 2x² – xy – y² в замкнутой области, заданной системой неравенств: х £ 1, у ³ 0, у £ х.

Решение:

1. Область представляет собой треугольник ОАВ (рис.12), причем

О (0, 0), А (1, 0), В (1, 1). Находим стационарные точки внутри области:

f ¢_x = - 4x – y, f ¢_y = -x – 2y; f ¢_x = 0, f ¢_x = 0, f ¢_y = 0, при х = 0, у = 0;

f (0, 0) =3.

2. На стороне ОА: у = 0, 0£ х £ 1 функции z = f (x, 0) = 3 – 2x² зависит от одной переменной х; z¢ (x)= -4x, z²(x) = -4, z¢(x) = 0 при х = 0; z²(0) = -4<0, x=0 – точка максимума: z (0) = f (0, 0) = 3.

3. На прямой АВ: х = 1, 0£ у £ 1, функция z = f (1, y) = 3 – 2 – y – y² =

= 1 – y – y² зависит только от y; z¢ (y) = -1 – 2y, z ¢ (y) = 0 при

y = -1/2, но эта точка не принадлежит отрезку АВ.

4. На стороне ОВ: у = х, 0 £ х £ 1 функция зависит только от х: z = f (x, x) = 3 – 2x² – x² – x²= 3 – 4x² , z ¢(x) = -8x, z ²(x) = -8, z = 0 при х = = 0, z ²(0) = -8 < 0, f (0, 0) = 3.

Вычисляем значения функции в точках А и В: f (A) = f (1, 0) = 1,

f (B) = f (1, 1) = -1.

Следовательно, в заданной области наименьшее значение данной функции равно –1, а наибольшее равно 3.

<12 3 4 5 6 7 >

Дата добавления: 2020-07-18; просмотров: 410;