В дифференциальной форме.
Применим названные законы для малого контура l0, ограничивающего некоторую поверхность DS, сквозь которую проходит ток Di (либо магнитный поток DФ). Стягивая контур l0, в точку, т.е. устремляя DS к нулю, рассмотрим пределы отношений обеих частей уравнений к величине DS, при ее стремлении к нулю:
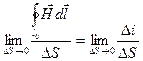 ;
; 
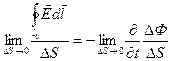
(В законе электромагнитной индукции в правой части стоит частная производная по времени, так как поток изменяется и во времени и за счет уменьшения размеров площадки DS, охваченной контуром интегрирования).
Для правой части закона полного тока можем записать:
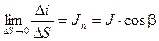 ,
,
где b – угол между вектором плотности тока и нормалью к поверхности, ограниченной контуром интегрирования lo. Предел отношения в левой части уравнения называется проекцией ротора вектора на ту же нормаль:
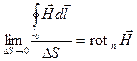 .
.
Ориентируя нормаль к площадке вдоль осей координат, получим равенство всех компонентов рассматриваемых векторов. Это означает, что оба вектора равны друг другу. Поэтому можем записать закон полного тока в векторной форме:
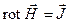 .
.
Ротор вектора также является вектором, поэтому записанное уравнение содержит три уравнения для проекций вектора и является инвариантным по отношению к системе координат. Записать это уравнение в декартовой системе координат можно с помощью оператора «набла», применяя операцию векторного умножения:




 =
=
= (  )
) 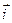 + (
+ ( 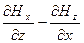 )
) 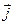 + (
+ (  )
) 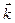 .
.
В скобках записаны проекции вектора плотности тока на оси координат:
Jx= 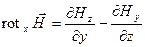 ; Jy=
; Jy= 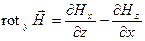 ; Jz=
; Jz= 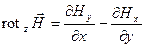 .
.
По аналогии запишем выражение для закона электромагнитной индукции:
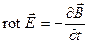 .
.
Оно также содержит три уравнения для проекций.
Дата добавления: 2021-02-19; просмотров: 567;











