Дифференцирующее звено с замедлением.

Звено описывается уравнением:

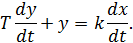
Звено можно условно представить в виде двух включенных последовательно звеньев – идеального дифференцирующего и апериодического первого порядка.

На рис 10 изображены примеры дифференцирующих звеньев с замедлением. Наиболее часто употребляются электрические цепи (рис 10, а и б). В некоторых случаях используются дифференцирующие устройства, состоящие из гидравлического демпфера и пружины (рис. 10, в).

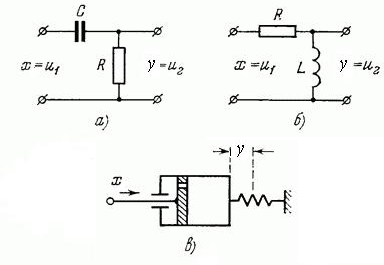
Рис. 10. Примеры дифференцирующих звеньев с замедлением

Составим, например, уравнение для дифференцирующего конденсатора (рис. 10, а). Ток в рассматриваемой цепи определяется уравнением:

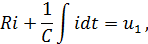
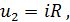
откуда

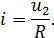
Отсюда, решая эти уравнения относительно тока i, получим

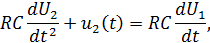
Зная, что RC = T, получаем уравнение

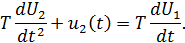
Форсирующее звено.

Звено описывается уравнением:

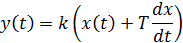
Такое звено не существует в природе, его получают искусственно.

Инерционно-форсирующее звено.

Звено описывается уравнением:

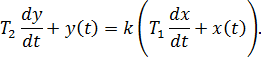
Примером таких звеньев могут служить пассивные цепочки (рис.11):

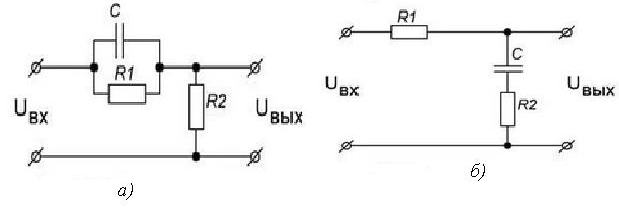
Рис. 11. Пассивные RC-цепочки

В первой схеме преобладает форсирующий эффект (т.к. T₁>T₂), а во второй – инерционный (т.к. T₂>T₁).