Режимы работы электрических двигателей

Существует три основных номинальных режима работы:

1) S1 – продолжительный режим работы при номинальной нагрузке. Характеризуется тем, что нагрев двигателя достигает установившегося значения. К таким режимам относятся режимы проводов редко включаемых. Различают два вида продолжительной работы:

а) с неизменной нагрузкой (двигатели насосов, транспортеров, вентиляторов с неизменной нагрузкой).

б) с изменяющейся нагрузкой (двигатели прокатных, металлорежущих станков).

2) S2 – кратковременный номинальный режим, где периоды номинальной нагрузки чередуется с периодами отключения. Периоды нагрузки таковы, что машина не нагревается до температуры установившегося значения. Периоды отключения – пауза такова, что двигатель успевает охладиться. Номинальные периода таковы: 10, 30, 60, 90 минут. В условном обозначении режима указывается время включения (S2 – 30мин). В таком режиме работают приводные двигатели шлюзов, заслонок и других запорных устройств, регулирующих подачу рабочего вещества.

3) S3 – повторно-кратковременный режим. При этом режиме время подключения двигателя и время паузы не длительны. Машина не достигает установившегося значения температуры нагрева. Общее время работы двигателя разделяется на периодические повторяющиеся циклы.

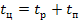
Этот режим характеризуется относительной продолжительностью включения (ПВ)

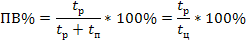
Стандартом предусмотрены номинальные повторно-кратковременный режимы с периодами включения промежутками 15% 25% 40% 60%. В условном обозначении режима указывают величину включения, например S3-40%.

Кроме этих трех режимов стандартом предусмотрено еще пять дополнительных режимов. Четвертый и пятый режимы повторно-кратковременные с отключением или торможением и отключением двигателя. Шестой-восьмой режимы без выключения двигателя после отключения нагрузки, предусматривается режим Х.Х.

Вопросы теории регулирования для линейных систем электропривода

Основные понятия теории систем автоматического регулирования.

1. Выходная величина системы – независимая переменная различной физической природы, определяющая возможные направления изменения выходной величины.

2. Выходная величина – зависимая величина определяющая параметры переменных или переменной поступающих на рабочую машину или в силовые каналы связи с рабочей машиной. Под выходной величиной для электрического привода может подразумеваться ток, напряжение, скорость вращения и т.д.

Выходной величиной может служить скорость вращения вала механизма, угол поворота и т.д.

Всякий привод можно представить в виде отдельных последовательно соединенных звеньев участвующих в последовательном преобразовании входной величины и подачи ее на вход следующего звена. Звенья, участвующие в преобразовании входной величины до уровня выходного называется динамическими звеньями. Под динамическим звеном понимают устройство любого физического вида и конструктивного оформления, но описываемого определенными дифференциальными уравнениями, в связи с этим классификация звеньев проводится по виду дифференциального уравнения. Однако одно и то же дифференциальное уравнение может описывать разнообразное устройство (механическое, гидравлическое, электрическое). Если обозначить входную величину через X₁, а выходную через Х₂ возмущающее воздействие через функцию f(t), то можно обозначить f(t)

Х₁ Х₂

Пусть звено описывается дифференциальным уравнением, представленным в стандартной форме:

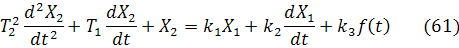
При нулевых начальных условиях т.е для t<0,

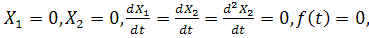может быть найдена передаточная функция звена как отношение изображения по Лапласу выходной и входной величин

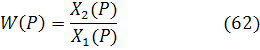
P – комплексный оператор.

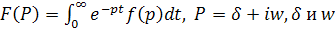– действительное число

Для выражения (61) передаточная функция звена имеет вид:

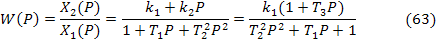
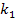- Коэффициент передачи звена

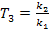– постоянная времени

В общем случае передаточная функция является дробно-рациональной функцией аргумента P и ее можно представить в виде отношения двух многочленов, а именно в виде, где Q(P) и P(p) – многочлены степеней m и n.

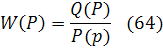
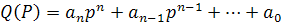
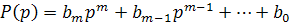
Многочлен знаменателя P(p) – называется характеристическим многочленом дифференциального уравнения рассматриваемого звена.

В общем случае передаточная функция получается из дифференциального уравнения, в котором описываются процессы, проходящие в рассматриваемом звене, если P=0, то передаточная функция превращается в коэффициент усиления.

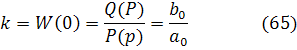
Во всех физически реализуемых системах выполняется условие m≤n