Осмотическое давление раствор ВМС

Как любые высокодисперсные системы, частицы которых подвержены тепловому движению, растворы ВМС обладают осмотическим давлением. Оно определяется концентрацией полимера, но практически всегда имеет очень малое значение даже в сравнительно концентрированных растворах. Это объясняется тем, что вследствие большой средней молярной массы число частиц дисперсной фазы в единице объема раствора полимера на несколько порядков меньше числа молекул в растворах низкомолекулярных соединений с аналогичной массовой долей растворенного вещества.

Однако, даже в сравнительно разбавленных растворах ВМС измеренное осмотическое давление (кривая 1 на рис. 75) оказывается большим, чем вычисленное по уравнению Вант-Гоффа (р_осм. = cRT) (кривая 2 на рис. 75).

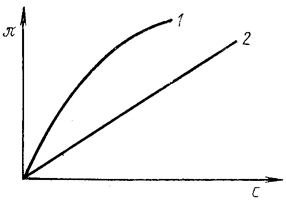
Рис. 75. Зависимость осмотического давления от концентрации раствора ВМС: 1 – определенная экспериментально; 2 – рассчитанная по уравнению Вант-Гоффа.

Отклонение это оказывается более заметным в растворах с гибкими макромолекулами. Объясняется это тем, что для длинных гибких макромолекул характерна так называемая сегментарная форма молекулярно-кинетического движения. Отдельные части макромолекулы (сегменты), расположенные сравнительно далеко друг от друга, оказываются независимыми в своем тепловом движении. Это приводит к тому, что макромолекула ведет себя в растворе как несколько молекул меньшего размера или несколько отдельных кинетических элементов. Чем более гибкой и ассиметричной является макромолекула в растворе, тем больше измеренное осмотическое давление отличается от теоретически вычисленного и тем сильнее оно возрастает при увеличении концентрации. Чтобы использовать закон Вант-Гоффа, в него нужно для каждого полимера вводить свой поправочный коэффициент β (определяется опытным путем), учитывающий форму макромолекул в растворе, их гибкость и сродство к растворителю.

р_осм. = 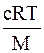+ βс²

где с – весовая концентрация полимера; М – средняя молярная масса полимера.