Линеаризации в области ограничений
Приведение ЗНП к виду ЗЛП может быть получено, если в целевую функцию ввести дополнительные переменные, а соотношение (9.20) отнести в область ограничений
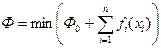 = = 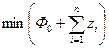
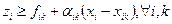 . .
| (9.22) |
Действительно, целевая функция тем меньше, чем меньше 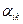 , которые, в свою очередь, могут снижаться до тех пор, пока не станут равными линейному представлению исходных нелинейных функций. Таким образом, несмотря на то, что минимизируется сумма введенных переменных, реально минимизируются нелинейные функции.
, которые, в свою очередь, могут снижаться до тех пор, пока не станут равными линейному представлению исходных нелинейных функций. Таким образом, несмотря на то, что минимизируется сумма введенных переменных, реально минимизируются нелинейные функции.
Пример. Получить решение ранее рассмотренной задачи оптимального распределения нагрузки Рн=200 между двумя параллельно работающими агрегатами.
Решение. Расходные характеристики представлены кусочно-линейными функциями
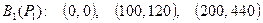 ;
;
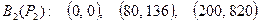 .
.
Угловые коэффициенты αk - 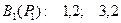 ;
; 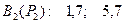
2. Представление задачи в виде линейного программирования
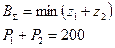 ,
,
а также

Решение данной задачи ЛП: 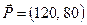 довольно далеко от того, что было получено методом Лагранжа. Причина – грубая (два интервала) аппроксимация. Для получения более точного решения требуется либо увеличить число интервалов, либо одним из интервальных узлов выбрать точку достаточно близкую к решению. В частности если принять
довольно далеко от того, что было получено методом Лагранжа. Причина – грубая (два интервала) аппроксимация. Для получения более точного решения требуется либо увеличить число интервалов, либо одним из интервальных узлов выбрать точку достаточно близкую к решению. В частности если принять
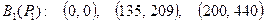
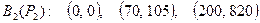 ,
,
то будет получено решение 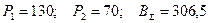
Результат совпадает с ранее полученным результатом.
Следует заметить, что во всех приведенных решениях одна из мощностей совпадает с интервальным узлом. Это – специфика ЛП – решение находится в вершине симплекса.
Дата добавления: 2020-07-18; просмотров: 548;











