Способы задания длины шага

Второй проблемой в организации итерационного цикла методами нелинейного программирования является выбор шага. Наиболее желательным является шаг l_опт, который приводит к минимуму функции по заданному направлению. Однако в общем случае найти этот шаг практически не представляется возможным. Отсюда используются две стратегии выбора шага: постоянство шага на некотором числе итераций и его уменьшение для достижения необходимой точности на конечном этапе расчетов; псевдооптимальный шаг, определяемый на базе некоторого числа предварительных расчетов.

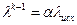При первой стратегии (постоянный шаг), , где a - вводимая на конечном этапе константа, как правило, меньшая единицы, чаще всего a = 0,5. Для обеспечения сходимости процесса вычислений, чтобы выполнялся критерий 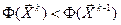, необходим контроль правильного задания длины шага. При нарушении критерия (см. выше) длину шага необходимо уменьшить. Уменьшение шага выполняется до тех пор пока не выполнится критерий 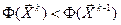или до выполнения критериев окончания расчетов.

Достоинство метода – малый объем вычислений на итерации (шаге). Недостаток – при неудачно выбранных 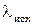и a количество шагов может быть достаточно велико и в целом объем и время расчетов недопустимо большие.

При втором подходе (оптимальный или псевдооптимальный шаг) длина шага 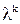выбирается из условия обеспечения максимального уменьшения целевой функции в заданном направлении.

Зависимость Ф(l) может быть сложной, нелинейной и многоэкстремальной и находить ее глобальный минимум неприемлемо, поэтому оптимальный шаг вычислить практически невозможно. Для оценки оптимального шага зависимость Ф(l) аппроксимируют, например, полиномом второй степени

.

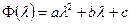Псевдооптимальная длина шага определяется из условия:

.

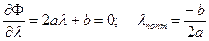Параметры a,b,c параболы Ф(l) можно найти по трем точкам l=0,1,2 (рис. 9.8). В качестве узлов аппроксимации принимаются значения 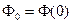, , 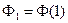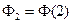в точках 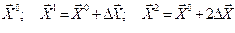. Подстановка 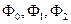в 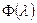позволяет получить СЛУ, из которой нетрудно определить искомые параметры

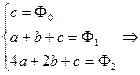
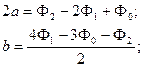
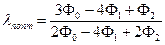
(9.23)

Значения l=1,2 не всегда обеспечивают корректные результаты. Величина 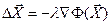из-за большого градиента может быть настолько большой, что новый вектор 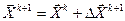выйдет за пределы ОДЗ. В этом случае шаг необходимо масштабировать, например 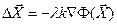, k<1.