Полная линейная комбинация
Одним из путей приведения ЗНП к ЗЛП является представление нелинейной функции 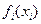 полной линейной комбинацией вновь вводимых интервальных переменных (рис. 9.5) , например при минимизации
полной линейной комбинацией вновь вводимых интервальных переменных (рис. 9.5) , например при минимизации
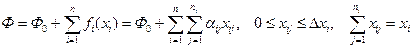
| Рис. 9.5. Дополнительные переменные |
 Правомочность такой аппроксимации заключается в том, что при минимизации из суммы
Правомочность такой аппроксимации заключается в том, что при минимизации из суммы 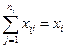 в первую очередь выбираются те
в первую очередь выбираются те 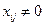 , которым соответствуют меньшие коэффициенты крутизны
, которым соответствуют меньшие коэффициенты крутизны 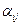 , что обеспечивает непрерывность последовательности переменных. В результате решения ЗЛП первые
, что обеспечивает непрерывность последовательности переменных. В результате решения ЗЛП первые 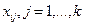 будут равны своим предельным значениям,
будут равны своим предельным значениям, 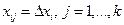 , а последняя, не равная нулю переменная может быть меньше предельной
, а последняя, не равная нулю переменная может быть меньше предельной 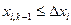 .
.
. В задаче оптимального распределения мощности нагрузки
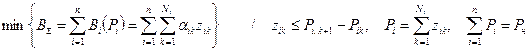
Рассматриваемая задача ЛП может быть представлена в виде.
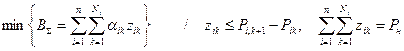
| (9.19) |
Пример. Получить оптимальное распределение нагрузки Рн=200 между двумя параллельно работающими агрегатами с расходными характеристиками
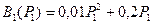 и
и 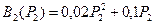 .
.
Представление задачи в виде ЗНП
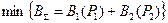 при условии
при условии 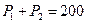 .
.
Ее решение методом Лагранжа (читателю предлагается получить его самостоятельно)
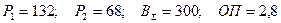 .
.
Кусочно-линейная аппроксимация расходных характеристик (представление в виде пар (Рik,Вik))
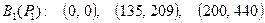 ;
;
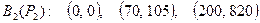 .
.
Здесь угловые коэффициенты 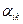 -
- 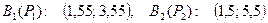 .
.
ЗЛП имеет вид
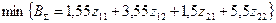 ;
;
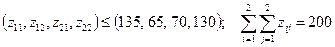 .
.
Решение. 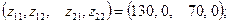
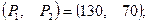
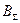 =306,5.
=306,5.
Дата добавления: 2020-07-18; просмотров: 526;











