Пример решения УУН методами нелинейного программирования

<67 68 69 70 71 7273>

Пример: Методами нелинейного программирования выполнить некоторое число итерации для решения нелинейных УУН из примера, рассмотренного в п.6.1

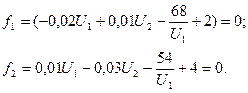
Метод покоординатной оптимизации

Шаг 1. . ;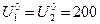

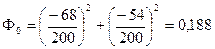На данном шаге варьируется напряжение первого узла, .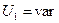

Определение псевдооптимального шага

; .

: ;

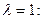
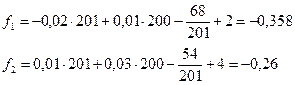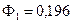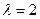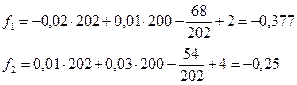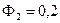
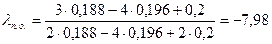
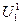=200-7,98=192,02

Шаг 2. .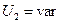

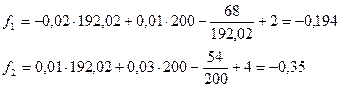Ф₀=0,16<0,2

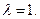
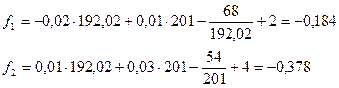
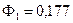
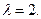
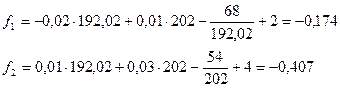
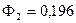
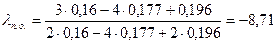
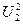=200-8,71=191,29

Вторая и третья итерации представлены в табл. 9.3. Здесь следует обратить внимание на то, что в процессе итерационных расчетов уменьшается не только целевая функция (0,188; 0,09; 0,029; 0,09; 0,03), но и псевдооптимальный шаг(-9,42; -5,39; -3,08). Однако это не правило. Шаг может и возрастать, как это имеет место, например, при переходе от первой ко второй итерации (-7,98; -9,42;).

Напомним, что точное решение в данной задаче 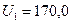и .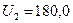

Таблица 9.3

U	e	λ				U	e	λ				U
192,02		f₁	-0,282	-0,300	-0,318	182,60		f₁	-0,112	-0,102	-0,092	182,60
191,29		f₂	-0,101	-0,091	-0,081	191,29		f₂	-0,195	-0,223	-0,252	186,45
		Ф	0,090	0,098	0,108			Ф	0,050	0,060	0,072
		λ_попт	-9,42			λ_попт	-4,84
U	e	λ				U	e	λ				U
182,60		f₁	-0,160	-0,178	-0,196	177,21		f₁	-0,064	-0,054	-0,044	177,21
186,45		f₂	-0,057	-0,047	-0,037	186,45		f₂	-0,111	-0,139	-0,168	183,69
		Ф	0,029	0,034	0,040			Ф	0,016	0,022	0,030
		λ_попт	-5,39			λ_попт	-2,76

Градиентный метод.

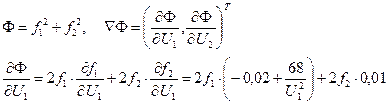
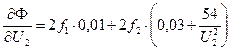
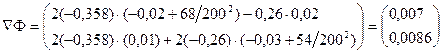Две итерации метода приведены в табл. 9.4.

Нетрудно видеть, что снижение функционала в градиентном методе более эффективное, нежели в методе покоординатного спуска.

Таблица 9.4

U		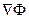λ				U		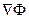λ				U
	0,007	f₁	-0,34	-0,34	-0,34	187,1	0,01	f₁	-0,26	-0,26	-0,26	182,09
	0,0086	f₂	-0,27	-0,27	-0,27	184,1	-0,008	f₂	0,05	0,05	0,06	188,03
		Ф	0,19	0,19	0,19			Ф	0,07	0,07	0,07
		λ_попт	-1834			λ_попт	-469